Question

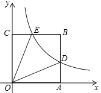
【题目】平面直角坐标系中，正方形OABC如图放置，反比例函数的图像交AB于点D，交BC于点E，已知A（，0），∠DOE=30°，则k的值为（ ）

A.B.C.3D.3

Answer 1

【答案】B

【解析】

由四边形ABCO是正方形，得到OC=OA，∠OCB=∠OAD=90°，设D（，），E（，），求得CE=AD=，根据全等三角形的性质得到∠COE=∠AOD，根据直角三角形的性质得到D的坐标，即可得到答案；

解：∵四边形ABCO是正方形，
∴OC=OA，∠OCB=∠OAD=90°，

A（，0），

∴，

设D（，），E（，），

∴CE=AD=，

∴△COE≌△AOD（SAS），
∴∠COE=∠AOD，
∵∠DOE=30°，∠AOC=90°，
∴∠AOD=∠COE=30°，

∴ ，

∴D（，1），

∴，

∴；

故选：B．