题目内容
【题目】某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg)销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①y与x满足一次函数关系,且当x=32时,y=39;x=40时,y=35.②m与x的关系为m=5x+50.
(1)y与x的关系式为______;
(2)当34≤x≤50时,求第几天的销售利润W(元)最大?最大利润为多少?
(3)若在当天销售价格的基础上涨a元/kg(0<a<10),在第31天至42天销售利润最大值为6250元,求a的值.
【答案】(1)y=﹣![]() x+55;(2)当x=34时,Wmax=4400元;(3)a=8.
x+55;(2)当x=34时,Wmax=4400元;(3)a=8.
【解析】
(1)依据题意利用待定系数法,易得出y与x的关系式为:y=-![]() x+55;
x+55;
(2)根据销售利润=销售量×(售价﹣进价),列出每天的销售利润W(元)与销售价x(元/箱)之间的函数关系式,再依据函数的增减性求得最大利润;
(3)要使第31天到第42天的日销售利润W(元)随x的增大而增大,列方程即可得到结论.
(1)依题意,当x=32时,y=39;x=40时,y=35,
设y=kx+b,
则有![]() ,解得
,解得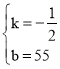 ,
,
∴y与x的关系式为:![]() ,
,
故答案为:![]() ;
;
(2)根据题意得,W=(y﹣18)m=![]() =
=![]() ,
,
∵![]() ,抛物线开口向下,
,抛物线开口向下,
∴当![]() 时,W随x的增大而减小,
时,W随x的增大而减小,
故当x=34时,Wmax=4400元;
(3)根据题意得,W![]()
![]() ,
,
∵![]() ,抛物线开口向下,
,抛物线开口向下,
对称轴为:![]() ,
,
∵![]() ,
,
∴32<32+a<42,
∵![]() 时,销售利润最大值为6250元,
时,销售利润最大值为6250元,
∴当![]() 时,Wmax=
时,Wmax=![]() =6250,
=6250,
解得:![]() 或
或![]() (舍),
(舍),
∴![]() .
.

练习册系列答案
相关题目