题目内容
【题目】已知y关于x的函数表达式是![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
A.若![]() ,函数的最大值是5
,函数的最大值是5
B.若![]() ,当
,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
C.无论a为何值时,函数图象一定经过点![]()
D.无论a为何值时,函数图象与x轴都有两个交点
【答案】D
【解析】
将a的值代入函数表达式,根据二次函数的图象与性质可判断A、B,将x=1代入函数表达式可判断C,当a=0时,y=-4x是一次函数,与x轴只有一个交点,可判断D错误.
当![]() 时,
时,![]() ,
,
∴当![]() 时,函数取得最大值5,故A正确;
时,函数取得最大值5,故A正确;
当![]() 时,
时,![]() ,
,
∴函数图象开口向上,对称轴为![]() ,
,
∴当![]() 时,y随x的增大而增大,故B正确;
时,y随x的增大而增大,故B正确;
当x=1时,![]() ,
,
∴无论a为何值,函数图象一定经过(1,-4),故C正确;
当a=0时,y=-4x,此时函数为一次函数,与x轴只有一个交点,故D错误;
故选D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
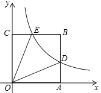
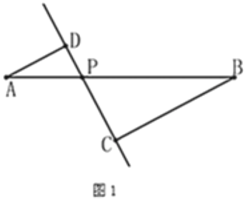
【题目】如图1,线段![]() 及一定点
及一定点![]() ,
,![]() 是线段
是线段![]() 上一动点(
上一动点(![]() 、
、![]() 除外),作直线
除外),作直线![]() ,使
,使![]() 于点
于点![]() ,作直线
,作直线![]() ,使
,使![]() 于点
于点![]() .已知
.已知![]() ,
,![]() ,设
,设![]() ,
,![]() ,数学学习小组根据学习函数的经验,对
,数学学习小组根据学习函数的经验,对![]() 与
与![]() 之间的内在关系进行探究.
之间的内在关系进行探究.
(1)写出y与![]() 之间的关系和
之间的关系和![]() 的取值范围;
的取值范围;
活动操作:
(2)①列表,根据(1)的所求函数关系式讲算并补全表格
| 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
|
| 1.8 | 9 | 21 |
②描点:根据表格中数值,继续在图2中描出剩余的三个点![]() ;
;
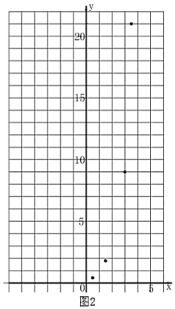
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考:
(3)请你结合函数的图象,写出该函数的一条性质或结论.
(4)将该函数图象向上移3个单位,再向左平移4个单位后,直接写出平移后的函数关系式和![]() 的取值范围.
的取值范围.