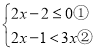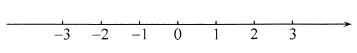题目内容
【题目】某公司经过市场调查，发现某种运动服的销量与售价是一次函数关系，具体信息如表：
已知该运动服的进价为每件150元．
（1）售价为x元，月销量为y件．
①求y关于x的函数关系式：
②若销售该运动服的月利润为w元，求w关于x的函数关系式，并求月利润最大时的售价；
（2）由于运动服进价降低了a元，商家决定回馈顾客，打折销售，这时月销量与调整后的售价仍满足（1）中函数关系式．结果发现，此时月利润最大时的售价比调整前月利润最大时的售价低15元，则a的值是多少？
【答案】（1）①
；②
元；（2）30元
【解析】
（1）①设y关于x的函数关系式为y=kx+b，由待定系数法求解即可；
②月利润w=（x-150）（-2x+600），整理并配方，然后根据二次函数的性质可得答案；
（2）设调整后的售价为t元，则调整后的单件利润为（t-150+a）元，销量为（-2t+600）件，写出月利润关于x的函数，并根据二次函数的性质得出月利润最大时的t值，从而得出关于a的方程，解出a即可．
解：（1）①设y关于x的函数关系式为y=kx+b，把（200，200），（210，180）
代入得：
解得：
，
∴y关于x的函数关系式为y=-2x+600；
②月利润w＝（x﹣150）（﹣2x+600）＝﹣2x2+900x﹣90000
＝﹣2（x﹣225）2+11250．
∵﹣2＜0，
∴w为开口向下的抛物线，
∴当x＝225时，月最大利润为11250元；
∴w关于x的函数关系式为w＝﹣2x2+900x﹣90000，月利润最大时的售价为225元；
（2）设调整后的售价为t元，则调整后的单件利润为（t﹣150+a）元，销量为（﹣2t+600）件．
月利润w＝（t﹣150+a）（﹣2t+600）
＝﹣2t2+（900﹣2a）t+600a﹣90000，
∴当
时，月利润最大，则
＝210，
解得a＝30．
∴a的值是30元．
【题目】茶叶是安徽省主要经济作物之一，2020年新茶上市期间，某茶厂为获得最大利益，根据市场行情，把新茶价格定为400元/kg，并根据历年的相关数据整理出第x天（1≤x≤15，且x为整数）制茶成本（含采摘和加工）和制茶量的相关信息如下表．假定该茶厂每天制作和销售的新茶没有损失，且能在当天全部售出（当天收入=日销售额-日制茶成本）
制茶成本（元/kg） | 150+10x |
制茶量（kg） | 40+4x |
（1）求出该茶厂第10天的收入；
（2）设该茶厂第x天的收入为y（元）．试求出y与x之间的函数关系式，并求出y的最大值及此时x的值．
