题目内容
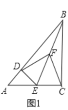
【题目】已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.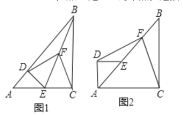
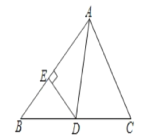
(1)如图1,当点D在AB上,且点E是AC的中点时,求CF的长.
(2)如图1,若点D落在AB上,点E落在AC上,证明:DF⊥CF.
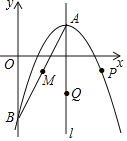
(3)如图2,当AD⊥AC,且E点落在AC上时,判断DF与CF之间的关系,并说明理由.
【答案】(1) CF=![]() ;(2)见解析; (3)DF与CF相等且垂直.证明见解析.
;(2)见解析; (3)DF与CF相等且垂直.证明见解析.
【解析】
(1)在直角△BCE中,利用“勾股定理和直角三角形斜边上的中线等于斜边的一半”解答;
(2)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=BF,根据∠DFE=2∠DCF,∠BFE=2∠BCF,得到∠EFD+∠EFB=2∠DCB=90°,DF⊥BF;
(3)DF与CF相等且垂直.如图2,延长DE交BC于点G,连接FG,易证DG⊥BC.构建矩形ADGC,结合矩形的性质推知△DEF≌△CGF,由该全等三角形的性质推知:DF与CF相等且垂直.
(1)如图1,∵AC=BC=4,点E是AC的中点,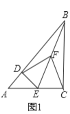
∴EC=2.
在直角△BCE中,BE2=BC2+CE2=20,
∴BE=![]() .
.
∵CF是直角△BCE斜边上的中线,
∴CF=![]() =
=![]() ;
;
(2)证明:如图1,∵∠ACB=∠ADE=90°,点F为BE中点
∴DF=![]() BE,CF=
BE,CF=![]() BE,
BE,
∴DF=CF.
∵△ABC和△ADE是等腰直角三角形,
∴∠ABC=45°
∵BF=DF,
∴∠DBF=∠BDF,
∵∠DFE=∠ABE+∠BDF,
∴∠DFE=2∠DBF,
同理得:∠CFE=2∠CBF,
∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,
∴DF⊥CF.
(3)DF与CF相等且垂直.
如图2,延长DE交BC于点G,连接FG,易证DG⊥BC.
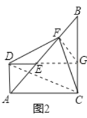
∵∠DEA=45°,
∴∠BEG=45°,∠DEF=135°.
又∵∠B=45°,
∴BG=EG.
∵点F是BE的中点,
∴FG=FE,FG⊥BE,∠EGF=45°,
∴∠FGC=∠EGF+EGC=135°,
∴∠DEF=∠CGF.
又∵∠ADE=90°,∠ACB=90°,DG⊥BC,
∴四边形ADGC是矩形,
∴AD=GC,
∴DE=GC,
∴△DEF≌△CGF(SAS),
∴∠DFE=∠CFG,DF=CF.
∵∠DFE+∠CFE=90°,
∴CF⊥DF,
∴DF与CF相等且垂直.

 习题精选系列答案
习题精选系列答案