题目内容
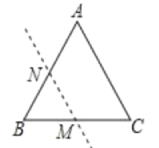
【题目】(1)(探究)如图,在等边△ABC中,AB=4cm,点M为边BC的中点,点N为边AB上的任意一点(不与点A,B重合).若点B关于直线MN的对称点B′恰好落在等边△ABC的边上,求BN的长.
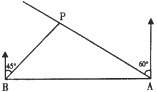
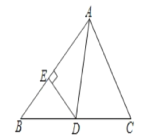
(2)(拓展)如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作DE⊥AB于点E,且sin∠DAB=![]() ,DB=3
,DB=3![]() .求AB的长.
.求AB的长.
【答案】探究1或2.;拓展7.
【解析】
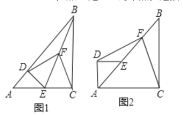
(1)如图1,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边AB上时,于是得到MN⊥AB,BN=BN′,根据等边三角形的性质得到=AC=BC,∠ABC=60°,根据线段中点的定义得到BN=![]() BM=1,如图2,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边A,C上时,则MN⊥BB′,四边形BMB′N是菱形,根据线段中点的定义即可得到结论.
BM=1,如图2,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边A,C上时,则MN⊥BB′,四边形BMB′N是菱形,根据线段中点的定义即可得到结论.
(2)由∠ABC=45°,过点D作DE⊥AB于点E,可知△BED是等腰直角三角形,由此可求得BE的长度,再由sin∠DAB=![]() ,可求得AD与AE的长度,进而求出AB的长度.
,可求得AD与AE的长度,进而求出AB的长度.
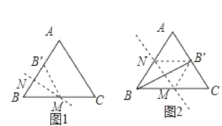
(1)如图1,当点B关于直线MN的对称点B′恰好落在等边三角形ABC的边AB上时,
则MN⊥AB,BN=BN′,
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=60°,
∵点M为边BC的中点,
∴BM=![]() BC=
BC=![]() AB=2,
AB=2,
∴BN=![]() BM=1,
BM=1,
如图2,当点B关于直线MN的对称点B′恰好落在等边三角形ABC的边A,C上时,
则MN⊥BB′,四边形BMB′N是菱形,
∵∠ABC=60°,点M为边BC的中点,
∴BN=BM=![]() BC=
BC=![]() AB=2,
AB=2,
故答案为:1或2.
(2)∵∠ABC=45°,过点D作DE⊥AB于点E
∴△BED是等腰直角三角形,
∴BE=ED=![]() DB=3,
DB=3,
∵sin∠DAB=![]() ,
,
∴![]() ,
,
∴AD=5,
∴由勾股定理可求得:AE=4,
∴AB=AE+BE=7.