题目内容
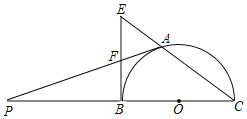
【题目】如图,长方形ABCD的边BC在直线l上,AD=5,AB=3,P为直线l上的点,且△ADP是腰长为5的等腰三角形,则BP=_____.

【答案】2.5或1或9或4.
【解析】
根据等腰三角形的性质,分为三种情况,画出图形,再根据勾股定理求出即可.
解:∵长方形ABCD的边BC在直线l上,AD=5,AB=3,
∴BC=AD=5,AB=DC=3,∠ABC=∠BCD=90°,
①如图1,作AD的垂直平分线EF交BC于P1,连接AP1,DP1,
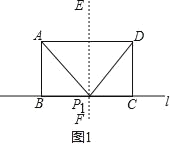
此时AP1=DP1,△ADP1是等腰三角形,BP1=CP1=![]() BC=2.5;
BC=2.5;
②如图2,以D为圆心,以AD为半径作圆,交直线l于P2,P3,
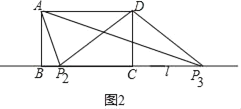
此时△ADP2和△ADP3是等腰三角形,
DP2=DP3=AD=5,
由勾股定理得:CP2=![]() =4,CP3=
=4,CP3=![]() =4,
=4,
∴BP2=5﹣4=1,BP3=5+4=9;
③如图3,以A为圆心,以AD为半径作圆,交直线l于P4,P5,
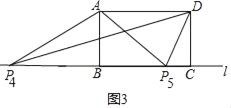
此时△ADP4和△ADP5是等腰三角形,
AP4=AP5=AD=5,
由勾股定理得:BP4=![]() =4,CP′=
=4,CP′=![]() =4,
=4,
即BP的长是2.5或1或9或4;
故答案为:2.5或1或9或4.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目