题目内容
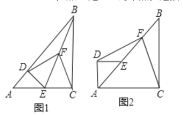
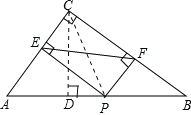
【题目】如图,已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连接EF,M为EF的中点.

(1)请判断四边形PECF的形状,并说明理由;
(2)随着P点在AB上位置的改变,CM的长度是否也会改变?若不变,求CM的长度;若有变化,求CM的变化范围.
【答案】(1)矩形;(2)![]()
【解析】
(1)首先根据勾股定理的逆定理判断三角形ABC是直角三角形,然后根据三个角都是直角的四边形是矩形即可得解;
(2)CM的长度会改变.连接PC,证得四边形PECF是矩形,得到EF=PC,求出PC的范围,即可得到得到EF的范围,即可得到CM 的范围.
(1)在△ABC中,AC=3,BC=4,AB=5.
∵AC2+BC2=32+42=52=AB2,∴∠ACB=90°.
∵PE⊥AC,PF⊥BC,∴∠PEC=∠ACB=∠CFP=90°,∴四边形PECF是矩形;
(2)CM的长度会改变,理由是:
连接PC,由(1)证得四边形PECF是矩形,∴EF=PC.
过点C作CD⊥AB,此时CD=PC且PC最小,∴PC![]() 2.4.
2.4.
∵点P是斜边AB上 (不与A、B重合),∴PC<BC=4,∴PC的范围是2.4≤PC<4,即EF的范围是2.4≤EF<4.
∵M为EF的中点,∴CM![]() EF,∴CM的范围是
EF,∴CM的范围是![]() .
.

练习册系列答案
相关题目