题目内容
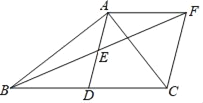
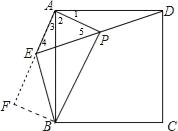
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() ,下列结论:①△APD≌△AEB;②点B到直线AE的距离为
,下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=
;③EB⊥ED;④S△APD+S△APB=![]() .其中正确结论的序号是_____.
.其中正确结论的序号是_____.
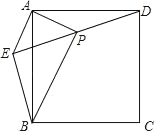
【答案】①③④
【解析】
作BF⊥AE于F,根据正方形的性质证明△APD≌△AEB即可判断①,根据△AEP为等腰直角三角形,得到∠APD=135°,再求出∠PEB=90°,即可判断③,根据Rt△PED中,求出BE=![]() ,再求出△BEF为等腰直角三角形,利用BF=
,再求出△BEF为等腰直角三角形,利用BF=![]() BE即可求出BF即可判断②,再根据S△APD+S△APB=S△AEB+S△APB=S四边形AEBP=S△AEP+S△PBE即可求出④的正确性.
BE即可求出BF即可判断②,再根据S△APD+S△APB=S△AEB+S△APB=S四边形AEBP=S△AEP+S△PBE即可求出④的正确性.
解:作BF⊥AE于F,如图,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵AP⊥AE,
∴∠EAP=90°,即∠2+∠3=90°,
∵∠1+∠2=90°,
∴∠1=∠3,
在△APD和△AEB中
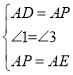 ,
,
∴△APD≌△AEB,所以①正确;
∵AE=AP,∠PAE=90°,
∴△AEP为等腰直角三角形,
∴∠4=∠5=45°,
∴∠APD=135°,
∵△APD≌△AEB,
∴∠AEB=∠APD=135°,
∴∠PEB=135°﹣∠4=90°,
∴BE⊥ED,所以③正确;
在Rt△PED中,BE=![]() ,
,
在Rt△BEF中,∵∠BEF=180°﹣∠AEB=45°,
∴△BEF为等腰直角三角形,
∴BF=![]() BE=
BE=![]() ×
×![]() =
=![]() ,所以②错误;
,所以②错误;
∵△APD≌△AEB,
∴S△APD=S△AEB,
∴S△APD+S△APB=S△AEB+S△APB=S四边形AEBP=S△AEP+S△PBE=![]() ×1×1+
×1×1+![]() ×
×![]() ×
×![]() =
=![]() ,所以④正确.
,所以④正确.
故答案为①③④.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目