题目内容
【题目】阅读下面材料
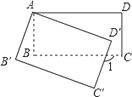
已知:如图,四边形ABCD是平行四边形;
求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(1)连接AC;
(2)作AC的垂直平分线EF分别交BC,AD于E,F.
(3)连接AE,CF
所以四边形AECF是菱形.
老师说:“小凯的作法正确”.
回答问题:
已知:在平行四边形ABCD中,点E、F分别在边BC、AD上______________________________________________.(补全已知条件)
【答案】EF垂直平分AC
【解析】
利用作法可得到EF垂直平分AC,再证明四边形AECF是菱形即可解答;
已知:在平行四边形ABCD中,点E、F分别在边BC、AD上,EF垂直平分AC;
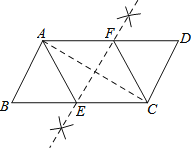
证明:∵EF垂直平分AC,
∴EA=EC,FA=FC,AC⊥EF,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DAC=∠ECA,
∵EA=EC,
∴∠ECA=∠EAC,
∴∠EAC=∠DAC,
∴AC平分EF,
即AC与EF互相垂直平分,
∴四边形AECF是菱形.
故答案为:EF垂直平分AC.

练习册系列答案
相关题目