题目内容
【题目】如图,两个以点O为圆心的同心圆,
图1 图2
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.
【答案】
(1)解:AC=BD,理由是:
过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,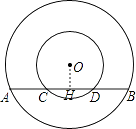
AH-CH=BH-DH,
即AC=BD
(2)解:连接OC,如图,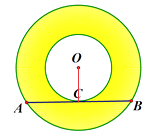
AB是小圆的切线,
OC⊥AB,则AC=BC
(3)解:如图,连接OB.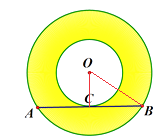
∵大圆的弦AB是小圆的切线, ∴OC⊥AB,AC=CB, ∴OB2-OC2=(20÷2)2=102 , ∵S圆环=S大-S小=πOB2-πOC2=π(OB2-OC2), ∴S圆环=100πcm2
【解析】(1)AC=BD,理由是:过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,根据等式的性质得出AH-CH=BH-DH,从而得出AC=BD ;
(2)连接OC,如图,根据切线的性质定理得出OC⊥AB,再根据垂径定理得出AC=BC ;
(3)连接OB.根据切线的性质定理得出OC⊥AB,再根据垂径定理得出AC=BC ,然后根据勾股定理及等式的性质得出OB2-OC2=(20÷2)2=102 ,然后根据S圆环=S大-S小=πOB2-πOC2=π(OB2-OC2)算出答案。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目