题目内容
【题目】某校举办“创建全国文明城市”知识竞赛，计划购买甲、乙两种奖品共30件．其中甲种奖品每件30元，乙种奖品每件20元．
（1）如果购买甲、乙两种奖品共花费800元，那么这两种奖品分别购买了多少件？
（2）若购买乙种奖品的件数不超过甲种奖品件数的3倍，如何购买甲、乙两种奖品，使得总花费最少？
【答案】（1）甲购买了20件，乙购买了10件；（2）购买甲奖品8件，乙奖品22件，总花费最少
【解析】
（1）设甲购买了x件乙购买了y件，利用购买甲、乙两种奖品共花费了800元列方程组，然后解方程组计算即可；
（2）设甲种奖品购买了a件，乙种奖品购买了（30-a）件，利用购买乙种奖品的件数不超过甲种奖品件数的3倍，然后列不等式后确定x的范围即可得到该校的购买方案．
解：（1）设甲购买了x件，乙购买了y件，
，
解得
，
答：甲购买了20件，乙购买了10件；
（2）设购买甲奖品为a件．则乙奖品为（30-a）件，根据题意可得：
30-a≤3a，
解得a≥
，
又∵甲种奖品每件30元，乙种奖品每件20元，
总花费=30a+20（30-a）=10a+600，总花费随a的增大而增大
∴当a=8时，总花费最少，
答：购买甲奖品8件，乙奖品22件，总费用最少.
【题目】某公园的门票价格如表：
购票人数 | 1～50 | 51～100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园，这两个部门人数分别为a和b（a≥b）．若按部门作为团体，选择两个不同的时间分别购票游览公园，则共需支付门票费为1290元；若两个部门合在一起作为一个团体，同一时间购票游览公园，则共需支付门票费为990元，那么这两个部门的人数a=_____；b=_____．
【题目】2020年是脱贫攻坚年，为实现全员脱贫目标，某村贫困户在当地政府支持帮助下，办起了养鸡场，经过一段时间精心饲养，总量为3000只的一批鸡可以出售．现从中随机抽取50只，得到它们质量的统计数据如下：
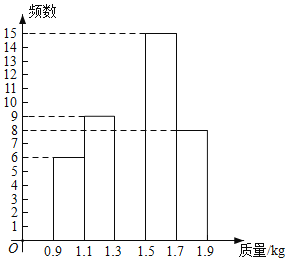
质量 | 组中值 | 数量（只） |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根据以上信息，解答下列问题：
（1）表中
______，补全频数分布直方图；
（2）这批鸡中质量不小于
的大约有多少只？
（3）这些贫因户的总收入达到54000元，就能实现全员脱贫目标．按15元
的价格售出这批鸡后，该村贫困户能否脱贫？
