题目内容
【题目】陕西省某甜瓜基地因“规模大、品质好、品牌亮”吸引了周边大批水果批发商订购,该基地对需要送货上门且购买量在![]() (含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
(含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
方案一:每千克![]() 元,免运费;
元,免运费;
方案二:每千克m元,客户需支付运费1200元.
(1)请分别写出这一天按方案一、方案二购买这种甜瓜的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)当购买量x在什么范围时,选择方案二比方案一付款少;
(3)已知5月某天批发价为每千克8元,某水果批发商计划用25000元在这一天购买尽可能多的这种甜瓜并需要送货上门,那么他在这两种方案中,应选择哪一种方案?
【答案】(1)方案一:![]() ,方案二:
,方案二:![]() ;(2)当购买量x的取值范围为
;(2)当购买量x的取值范围为![]() 时,选择方案二比方案一付款少;(3)他在这两种方案中,应选择方案二,见解析
时,选择方案二比方案一付款少;(3)他在这两种方案中,应选择方案二,见解析
【解析】
解:(1)方案一:![]() ,
,
方案二:![]() ;
;
(2)令![]() ,
,
解不等式,得![]() ,
,
![]() 当购买量x的取值范围为
当购买量x的取值范围为![]() 时,选择方案二比方案一付款少;
时,选择方案二比方案一付款少;
(3)当![]() 时,方案一:
时,方案一:![]() ,
,
方案二:![]() .
.
由题意得:
方案一可购买甜瓜![]() ,
,
方案二可购买甜瓜![]() .
.
![]() ,
,
![]() 他在这两种方案中,应选择方案二.
他在这两种方案中,应选择方案二.

【题目】小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
![]() .小云所住小区5月1日至30日的厨余垃圾分出量统计图:
.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
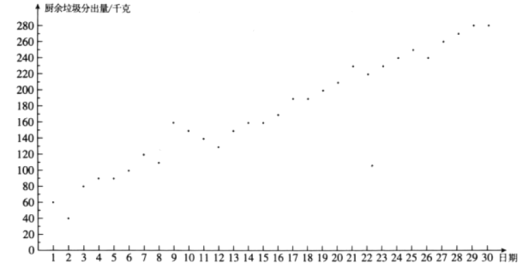
![]() .小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段 | 1日至10日 | 11日至20日 | 21日至30日 |
平均数 | 100 | 170 | 250 |
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为 (结果取整数)
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的 倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为![]() 5月11日至20日的厨余垃圾分出量的方差为
5月11日至20日的厨余垃圾分出量的方差为![]() ,5月21日至30日的厨余垃圾分出量的方差为
,5月21日至30日的厨余垃圾分出量的方差为![]() .直接写出
.直接写出![]() 的大小关系.
的大小关系.