Question

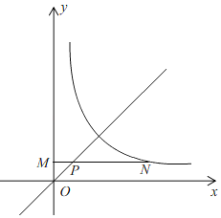
【题目】在平面直角坐标系xOy中，函数y=（x＞0）的图象与直线y=mx交于点A（2，2）．

（1）求k，m的值；

（2）点P的横坐标为n（n＞0），且在直线y=mx上，过点P作平行于x轴的直线，交y轴于点M，交函数y=（x＞0）的图象于点N．

①n=1时，用等式表示线段PM与PN的数量关系，并说明理由；

②若PN≥3PM，结合函数的图象，直接写出n的取值范围．

Answer 1

【答案】（1）4；1 （2）①见解析 ②

【解析】

（1）将点A坐标代入双曲线解析式中和直线解析式中，求解即可得出结论；

（2）① 先求出点M，N点坐标，即可得出结论；

② 先求出点P坐标，进而表示出点M，N的坐标，得出PM，PN，利用PN≥3PM建立不等式求解即可得出结论．

（1）∵ y=（x＞0）的图象与直线y=mx交于点A（2，2），

∴ k=2×2=4，2=2m，

∴ m=1，

即 k=4，m=1；

（2）①由（1）知，k=4，m=1，

∴ 双曲线的解析式为y=，直线OA的解析式为y=x，

∵ n=1，

∴ P（1，1），

∵ PM//x轴，

∴ M（0，1），N（4，1），

∴ PM=1，PM=4﹣1=3，

∴ PN=3PM；

② 由①知，如图，双曲线的解析式为y=，直线OA的解析式为y=x，

∵ 点P的横坐标为n，

∴ P（n，n），

∵ PM//x轴，

∴ M（0，n），N（，n），

∵ PN≥3PM，

∴ PM=n，PN=﹣n，

∵ PN≥3PM，

∴﹣n≥3n，

∴ 0＜n≤1．