题目内容
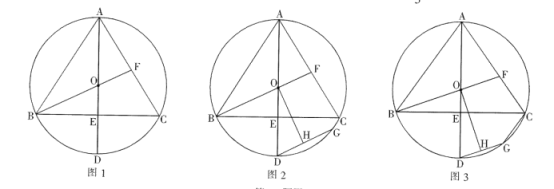
【题目】已知![]() 是
是![]() 的外接圆,AD为
的外接圆,AD为![]() 的直径,
的直径,![]() ,垂足为E,连接BO,延长BO交AC于点F.
,垂足为E,连接BO,延长BO交AC于点F.
(1)如图1,求证:![]() ;
;
(2)如图2,过点D作![]() ,交
,交![]() 于点G,点H为GD的中点,连接OH,求证:
于点G,点H为GD的中点,连接OH,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接CG,若![]() 的面积为
的面积为![]() ,求线段CG的长.
,求线段CG的长.
【答案】(1)见详解;(2)见详解;(3)CG=![]() .
.
【解析】
(1)先推出∠BAD=∠CAD,然后根据圆周角定理可得出∠BOD=2∠BAD=2∠CAD,根据∠BOD=∠AOF,可得出∠AOF=2∠CAD,根据∠BFC=∠AOF+∠CAD,即可证明结论;
(2)连接OG,证明△OBE≌△DOH,即可证明结论;
(3)连接AG,过A点作AM⊥CG于点M,过F点作FN⊥AD于点N,先推出DE=2OE,设OE=m,则DE=2m,OB=OD=OA=3m,AE=4m,根据勾股定理得出CE=BE=![]() ,再求出tan∠BOE=
,再求出tan∠BOE=![]() =
=![]() =
=![]() ,tan∠EAC=
,tan∠EAC=![]() =
=![]() =
=![]() ,根据tan∠AOF=tan∠BOE=
,根据tan∠AOF=tan∠BOE=![]() ,得出
,得出![]() =
=![]() ,设ON=a,则NF=
,设ON=a,则NF=![]() a,可得tan∠EAC=
a,可得tan∠EAC=![]() ,解出AN,根据AN+NO=AO,解出a=
,解出AN,根据AN+NO=AO,解出a=![]() m,再根据S△AOF=
m,再根据S△AOF=![]() ·OA·FN=
·OA·FN=![]() ,可求出m=1,可得出DH=1,OD=3, BE=CE=OH=
,可求出m=1,可得出DH=1,OD=3, BE=CE=OH=![]() ,AE=4,根据勾股定理可得AC=
,AE=4,根据勾股定理可得AC=![]() ,根据OD=OA,DH=HG,得出AG=2OH=
,根据OD=OA,DH=HG,得出AG=2OH=![]() ,推出cos∠ADG=cos∠ACM,即可求出CM=
,推出cos∠ADG=cos∠ACM,即可求出CM=![]() ,利用勾股定理可得AM=
,利用勾股定理可得AM=![]() ,GM=
,GM=![]() ,即可得出答案.
,即可得出答案.
解:(1)∵AD为![]() 的直径,
的直径,![]() ,
,
∴![]() ,BE=CE,
,BE=CE,
∴∠BAD=∠CAD,
∵∠BOD=2∠BAD,
∴∠BOD=2∠CAD,
∵∠BOD=∠AOF,
∴∠AOF=2∠CAD,
∵∠BFC=∠AOF+∠CAD,
∴∠BFC=2∠CAD+∠CAD=3∠CAD;
(2)连接OG,
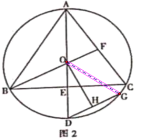
∵点H为GD的中点,OG=OD,
∴DH=GH,OH⊥DG,
∵AD⊥BC,
∴∠AEB=∠OHD=90°,
∵DG∥BF,
∴∠BOH=∠OHD=90°,
即∠DOH+∠BOD=90°,
∵∠BOD+∠OBE=90°,
∴∠OBE=∠DOH,
又∵OB=OD,
∴△OBE≌△DOH,
∴BE=OH;
(3)如图,连接AG,过A点作AM⊥CG于点M,过F点作FN⊥AD于点N,
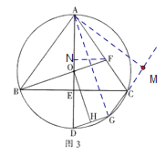
由(2)可知DH=OE,
∵DG=2DH=2OE,DG=DE,
∴DE=2OE,
设OE=m,则DE=2m,
∴OB=OD=OA=3m,
∴AE=4m,
在Rt△OBE中,BE=![]() =
=![]() ,
,
∴CE=BE=![]() ,tan∠BOE=
,tan∠BOE=![]() =
=![]() =
=![]() ,tan∠EAC=
,tan∠EAC=![]() =
=![]() =
=![]() ,
,
∵tan∠AOF=tan∠BOE=![]() ,
,
∴![]() =
=![]() ,
,
设ON=a,则NF=![]() a,
a,
∴tan∠EAC=![]() ,
,
∴AN=4a,
∵AN+NO=AO,
∴4a+a=3m,
∴a=![]() m,
m,
∴FN=![]() ×
×![]() m=
m=![]() m,
m,
∵S△AOF=![]() ·OA·FN=
·OA·FN=![]() ,
,
∴![]() ·3m·
·3m·![]() m=
m=![]() ,
,
∴m2=1,
∴m=±1,
∵m>0,
∴m=1,
∴DH=1,OD=3,由(2)得BE=CE=OH=![]() ,AE=4,
,AE=4,
在Rt△AEC中AC![]() =
=![]() ,
,
∵OD=OA,DH=HG,
∴AG=2OH=![]() ,
,
∵∠ADG+∠ACG=180°,∠ACM+∠ACG=180°,
∴∠ADG=∠ACM,
∴cos∠ADG=cos∠ACM,
∴![]() ,
,
∴![]() ,
,
∴CM=![]() ,
,
在Rt△ACM中,AM=![]() =
=![]() ,
,
在Rt△AGM中,GM=![]() =
=![]() ,
,
∴CG=GM-CM=![]() .
.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】4月23日是世界读书日,校文学社为了解学生课外阅读的情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
收集数据:从学校随机抽取20名,进行了每周用于课外阅读时间的调查,数据如下(单位:![]() ):
):
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分数段整理样本数据并补全表格:
|
|
|
| |
等级 |
|
|
|
|
人数 | 3 |
| 8 | 4 |
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 |
|
|
得出结论:
(1)请写出表中![]() _________;
_________;![]() _________
_________![]() ;
;![]() __________
__________![]() ;
;
(2)如果该校现有学生7500人,估计等级为“![]() ”的学生有_________名;
”的学生有_________名;
(3)假设平均阅读一本课外书的时间为![]() ,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?