题目内容
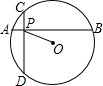
如图，半径为2
的⊙O内两条互相垂直的弦AB、CD交于点P，AB=8，CD=6，则OP=______．
| 5 |
作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，
由垂径定理得：OM2=（2
）2-42=4，ON2=（2
）2-32=11，
∵弦AB、CD互相垂直，
∴∠DPB=90°，
∵OM⊥AB于M，ON⊥CD于N，
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形，
∴OP=
=
=
．
故答案为：
．
由垂径定理得：OM2=（2
| 5 |
| 5 |
∵弦AB、CD互相垂直，
∴∠DPB=90°，
∵OM⊥AB于M，ON⊥CD于N，
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形，
∴OP=
| OM2+ON2 |
| 4+11 |
| 15 |
故答案为：
| 15 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
