题目内容
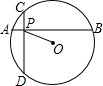
如图，BC是圆O的直径，AD垂直BC于D，
=
，BF与AD交于E，
求证：（1）AE=BE，
（2）若A，F把半圆三等分，BC=12，求AD的长．
 |
| BA |
|
| AF |
求证：（1）AE=BE，
（2）若A，F把半圆三等分，BC=12，求AD的长．
（1）证明：连AC，如图，
∵BC为直径，则∠BAC=90°，
∴∠C+∠ABC=90°，
又∵AD⊥BC，
∴∠BAE+∠ABC=90°，
∴∠C=∠BAE，
由
=
，可得∠C=∠ABF，
∴∠ABE=∠BAE，
∴AE=BE；
（2）∵A，F把半圆三等分，
∴∠ACB=30°，
在直角三角形ABC中，BC=12，则AB=
BC=6，AC=
AB=6
．
在直角三角形ADC中，AD=
AC=3
．
所以AD=3
．
∵BC为直径，则∠BAC=90°，
∴∠C+∠ABC=90°，
又∵AD⊥BC，
∴∠BAE+∠ABC=90°，
∴∠C=∠BAE，
由
|
| BA |
|
| AF |
∴∠ABE=∠BAE，
∴AE=BE；
（2）∵A，F把半圆三等分，
∴∠ACB=30°，
在直角三角形ABC中，BC=12，则AB=
| 1 |
| 2 |
| 3 |
| 3 |
在直角三角形ADC中，AD=
| 1 |
| 2 |
| 3 |
所以AD=3
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
