Question

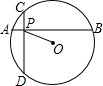
如图所示，AB是⊙○的一条弦，OD⊥AB，垂足为C，交⊙○于点D，点E在⊙○上，∠AOD=60°，OA=5．
（1）求∠DEB的度数；（2）求弓形ADB的面积．

Answer 1

（1）∵OD⊥AB
∴

AD

=

BD

，
∴∠DEB=

1

2

∠AOD=

1

2

×60°=30°；

（2）连接OB，
∵Rt△AOC中∠AOC=60°，OA=5，
∴∠OAC=30°，OC=

1

2

OA=

5

2

；AC=OA•cos∠OAC=5×

3

2

=

5 3

2

，
∵OD⊥AB，AOD=60°，
∴∠AOB=2∠AOC=120°，
∴S_弓形=S_扇形AOB-S_△AOB=

120×52×π

360

-

1

2

×5

3

×

5

2

=

100π-25 3

12

．