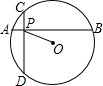
题目内容
如图所示，△ABC中，AC=BC，以AC为直径的⊙O交AB于E，作△BCA的外角平分线CF交⊙O于F，连接EF，求证：EF=BC．
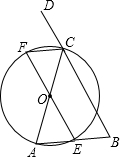
证明：∵CA=CB，
∴∠B=∠A，
又∵∠DCA=2∠FCA，∠DCA=∠A+∠B=2∠A，
∴∠FCA=∠A．
∴CF∥AB．
又∵∠FCA=∠FEA（同弧所对的圆周角相等），
∴∠FEA=∠B．
∴BC∥EF．
∴四边形CFEB为平行四边形．
∴EF=BC．
∴∠B=∠A，
又∵∠DCA=2∠FCA，∠DCA=∠A+∠B=2∠A，
∴∠FCA=∠A．
∴CF∥AB．
又∵∠FCA=∠FEA（同弧所对的圆周角相等），
∴∠FEA=∠B．
∴BC∥EF．
∴四边形CFEB为平行四边形．
∴EF=BC．
练习册系列答案
相关题目
