题目内容
【题目】等腰三角形![]() 中,
中,![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 在射线
在射线![]() 上,
上,![]() ,若
,若![]() ,线段
,线段![]() 的长度为_______.
的长度为_______.
【答案】8或4
【解析】
先根据题意画图.再BC上取一点F使BF=AE,连接DF,易证△DBF≌△DEA.从而得到AD=DF.然后再利用三角形外角性质定理,通过等量代换证明∠DFC=∠C,则可得DF=FC,从而将求AD转化为求FC.将已知线段长度代入,可求出AD的长度.
解:如图,在BC上取点F,使BF=AE,连接DF,
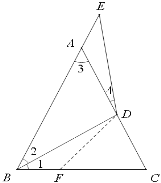
∵DB=DE,AB=AC
∴∠2=∠E,∠ABC=∠C
∵BD平分∠ABC
∴∠1=∠2
∴∠1=∠E
在△DBF与△DEA中
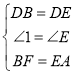 ,
,
∴△DBF≌△DEA(SAS)
∴∠BDF=∠4,AD=DF
∵∠BDC=∠2+∠3,∠3=∠E+∠4
∴∠BDC=∠2+∠E+∠4
∴∠FDC=∠BDC-∠BDF=∠2+∠E+∠4-∠4=∠2+∠E=∠2+∠1=∠ABC
∴∠FDC=∠C
∴DF=CF
∵BC=6,BF=AE=2
∴CF=BC-BF=6-2=4
∴AD=DF=4;
当点E在AB上,在BC延长线上取点F,使BF=AE=2,连接DF
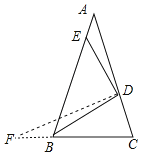
∵DE=DB,
∴∠DEB=∠DBE=∠DBC,
∴∠DBF=∠DEA,AE=BF,DB=DE
∴△AED≌△FBD(SAS)
∴AD=DF,∠A=∠F
∵AB=AC
∴∠ABC=∠C
∵∠A+∠C+∠ABC=180°,且∠F+∠C+∠FDC=180°
∴∠ABC=∠FDC
∴∠FDC=∠C
∴DF=FC=BF+BC=8
∴AD=8;
故答案为:4或8.

练习册系列答案
相关题目