��Ŀ����
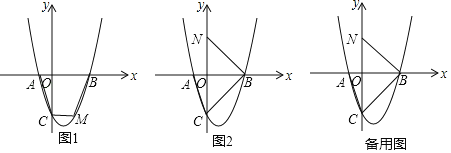
����Ŀ����֪����ͼ��������y��x2+bx+c��x���ཻ��AB���㣬��y���ཻ�ڵ�C����A����1��0������OC��3OA��
��1����գ�b���� ����c���� ����
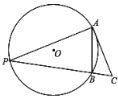
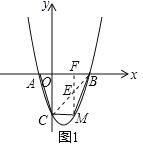
��2����ͼ1�У�����MΪ�������ϵ���������һ���㣬˳������AC��CM��MB�����ı���ACMB��������ֵ��
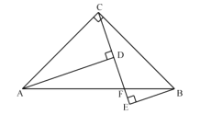
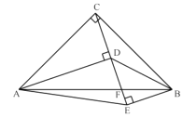
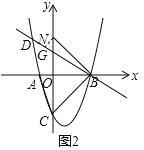
��3����ͼ2�У���ֱ��BC��x�ᷭ�۽�y���ڵ�N������B��ֱ�����������ཻ�ڵ�D������NBD����OCA����ֱ��д����D�����꣮
���𰸡���1����2����3����2��![]() ����3����D������Ϊ����
����3����D����������![]() ��
��![]() ����3��12����
����3��12����
��������
��1����A��1��0����OC��3OA���C���꣬�ѵ�A��C�����ô���ϵ�����������߽���ʽ�������b��c��ֵ��
��2������BC�����ı���ACMB�ֳɡ�ABC���BCM�����B���꣬�������ABC�����ֱ��BC����ʽ�����M������Ϊm������M��MF��x���ڵ�F����BC�ڵ�E����m��ʾEM�ij����ѡ�BCM�ֳɡ�BEM���CEM������ͣ��õ�����m�Ķ��κ�����ϵʽ���䷽���õ���BCM������ֵ����������ı���ACMB��������ֵ��
��3����OC��3OA���tan��OCA��ֵ�����N�����BN�ij�������N��GN��BN�����ݡ�NBD����OCA�ɵ�tan��NBD��![]() �������NG�ij��������ù��ɶ������BN�ij������G����Ϊ��s��t������s��t��ʾNG2��BG2��ֵ�����еù���s��t�ķ����飬�����������������ĵ�G����ֱ��BG����ʽ���������߽���ʽ���������鼴��õ�D���꣮
�������NG�ij��������ù��ɶ������BN�ij������G����Ϊ��s��t������s��t��ʾNG2��BG2��ֵ�����еù���s��t�ķ����飬�����������������ĵ�G����ֱ��BG����ʽ���������߽���ʽ���������鼴��õ�D���꣮
�⣺��1����A����1��0��
��OA��1
��OC��3OA��3
��C��0����3��
��������y��x2+bx+c������A��C
��![]() ��ã�
��ã�![]()
�ʴ�Ϊ����2����3��
��2����ͼ1������BC������M��MF��x���ڵ�F����BC�ڵ�E
�������߽���ʽΪy��x2��2x��3
�൱x2��2x��3��0ʱ����ã�x1����1��x2��3
��B��3��0����AB��3������1����4
��S��ABC��![]() ABOC��
ABOC��![]() ��4��3��6
��4��3��6
��ֱ��BC����ʽΪ��y��kx��3
�ѵ�B����ã�3k��3��0����ã�k��1
��ֱ��BC��y��x��3
�ߵ�MΪ�������ϵ��������ڵĵ�
�����M������m��m2��2m��3����0��m��3��
��E��m��m��3��
��EM��m��3����m2��2m��3������m2+3m������m��![]() ��2+
��2+![]()
��S��BCM��S��BEM+S��CEM
��![]() EMBF+
EMBF+![]() EMOF
EMOF
��![]() EM��BF+OF��
EM��BF+OF��
��![]() EMOB
EMOB
��![]() [����m��
[����m��![]() ��2+
��2+![]() ]
]
����![]() ��m��
��m��![]() ��2+
��2+![]()
��S�ı���ACMB��S��ABC+S��BCM��6��![]() ��m��
��m��![]() ��2+
��2+![]() ����
����![]() ��m��
��m��![]() ��2+
��2+![]()
���ı���ACMB��������ֵΪ![]() ��
��
��3������N��NG��BN����ֱ��BD�ڵ�G
���BNG����AOC��90��
��OC��3OA
��Rt��AOC��tan��OCA��![]()
�ߡ�NBD����OCA
��tan��NBD��tan��OCA��![]()
��Rt��BNG��tan��NBD��![]()
��B��3��0����C��0����3������ֱ��BC��x�ᷭ�۽�y���ڵ�N
��N��0��3��
��BN��![]()
��NG��![]() BN��
BN��![]()
��BG��![]()
���G������s��t��
��NG2��s2+��t��3��2��BG2����3��s��2+t2
��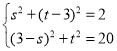 ��ã�
��ã�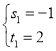 ,
,![]()
���G��������1��2����1��4��
��G����1��2������ֱ��BG����ʽΪy��ax+g
��![]() ��ã�
��ã�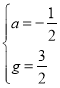
��ֱ��BG��y����![]() x+
x+![]()
��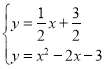 ��ã�
��ã�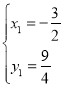 ,
,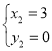 ������B��
������B��
��D����![]() ��
��![]() ��
��
��G��1��4��������ֱ��BG����ʽΪy��px+q
��![]() ��ã�
��ã�![]()
��ֱ��BG��y��-2x+6
��![]() ��ã�
��ã�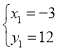 ,
,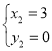 ������B��
������B��
��D ����3��12��
��������������NBD����OCA/span>����D����������![]() ��
��![]() ����3��12����
����3��12����

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�