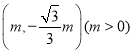题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 分别与x轴,y轴交于点
分别与x轴,y轴交于点![]() ,点C是第一象限内的一点,且
,点C是第一象限内的一点,且![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与x轴的另一交点为D.
两点,与x轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以![]() 四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
【答案】(1)二次函数的解析式为![]() ;(2)AB∥CD,证明见解析;(3)点N的坐标分别为(
;(2)AB∥CD,证明见解析;(3)点N的坐标分别为(![]() ,1),(
,1),(![]() ,1),(
,1),(![]() ,-1),(
,-1),(![]() -1).
-1).
【解析】
(1)求得点C的坐标,应用待定系数法即可求得抛物线的解析式.
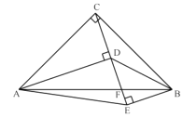
(2)根据勾股定理求出AC,CD,AD的长,从而根据勾股定理逆定理得到△ACD为直角三角形,∠ACD=90°,由∠BAC=90°,得出AB∥CD.
(3)由题意可知,要使得以A,B,M,N四点构成的四边形为平行四边形,只需要点N到x轴的距离与点B到x轴的距离相等.据此列出方程求解即可.
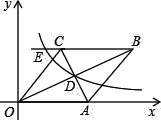
解:(1)由题意可求点A(2,0),点B(0,1).
过点C作CE⊥x轴,易证△AOB≌△ECA.
∴ OA=CE=2,OB=AE=1.
∴ 点C的坐标为(3,2).
将点A(2,0),点C(3,2)代入![]() ,
,
得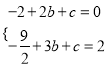 ,,解得
,,解得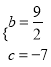 .
.
∴二次函数的解析式为![]() .
.
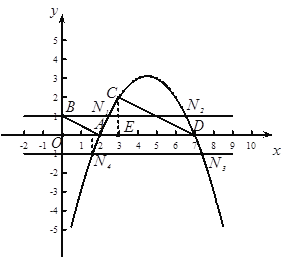
(2)AB∥CD.证明如下:
令![]() ,解得
,解得![]() .
.
∴ D点坐标为(7,0).
可求![]() .
.
∴△ACD为直角三角形,∠ACD=90°.
又∵∠BAC=90°,
∴ AB∥CD.
(3)如图,由题意可知,要使得以A,B,M,N四点构成的四边形为平行四边形,只需要点N到x轴的距离与点B到x轴的距离相等.
∵ B点坐标为(0,1),
∴ 点N到x轴的距离等于1.
可得![]() 和
和![]() .
.
解这两个方程得![]() .
.
∴点N的坐标分别为(![]() ,1),(
,1),(![]() ,1),(
,1),(![]() ,-1),(
,-1),(![]() ,-1).
,-1).

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目