题目内容
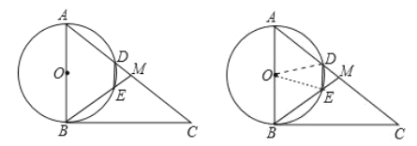
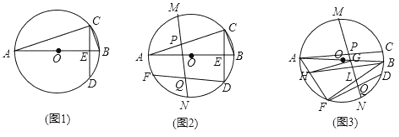
【题目】![]() 是
是![]() 直径,
直径,![]() 分别是上下半圆上一点,且弧
分别是上下半圆上一点,且弧![]() 弧
弧![]() ,连接
,连接![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,
(1)如图(1)求证:![]() ;
;
(2)如图(2)![]() 是弧
是弧![]() 一点,点
一点,点![]() 分别是弧
分别是弧![]() 和弧
和弧![]() 的中点,连接
的中点,连接![]() ,连接
,连接![]() 分别交
分别交![]() ,
,![]() 于
于![]() 两点,求证:
两点,求证:![]()
(3)如图(3)在(2)问条件下,![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,若
,若![]() 的面积等于
的面积等于![]() ,求线段
,求线段![]() 的长度
的长度
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由垂径定理即可证明;
(2)利用等弧所对的圆周角相等和三角形外角性质即可得到结论;
(3)由∠MPC=∠NQD可得:∠BGL=∠BLG,BL=BG,作BR⊥MN,GT⊥AF,HK⊥AB,证明:GH平分∠AGT,利用相似三角形性质和角平分线性质求得△AGT三边关系,再求出HK与GH,OS⊥MN,再利用相似三角形性质求出OS,利用勾股定理求MN即可.
解:![]() 证明:∵
证明:∵![]() ,AB为直径,
,AB为直径,
∴AB⊥CD
∴∠AEC=90°;
![]() 连接
连接![]() ,
,
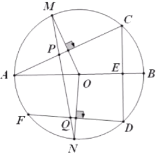
∵点M是弧AC的中点,点N是弧DF的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵OM=ON,
∴![]() ,
,
∵![]() ,
,
![]() ;
;
![]() 如图3,过G作GT⊥AF于T,过H作HK⊥AB于K,过B作BR⊥MN于R,过O作OS⊥MN于S,连接OM,设BG=m,
如图3,过G作GT⊥AF于T,过H作HK⊥AB于K,过B作BR⊥MN于R,过O作OS⊥MN于S,连接OM,设BG=m,
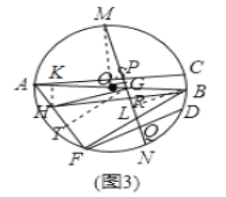
∵△ABH的面积等于8,AG=6
∴HK=![]() ,
,
∵![]() ,
,
∴∠BAC=∠BFD,由(2)得∠MPC=∠NQD
∴∠AGM=∠FLN
∴∠BGL=∠BLG
∴BL=BG,
∵BR⊥MN
∴∠ABR=∠FBR
∵GH⊥MN
∴GH∥BR
∴∠AGH=∠ABR
∵AB是直径,GT⊥AF
∴∠AFB=∠ATG=90°
∴GT∥BF,
又∵GH∥BR
∴∠TGH=∠FBR
∴∠AGH=∠TGH,
又∵HK⊥AG,HT⊥GT,
∴HT=HK=![]() ,
,
∵FH=BG=m,
∴FT=![]() ,
,
∵GT∥BF,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
代入解得:m=4;
∴AB=10,OM=5,GK=![]() ,HK=
,HK=![]() ,OG=1
,OG=1
∴GH=![]() ,
,
∵OS⊥MN
∴∠OSG=∠GKH=90°,GH∥OS
∴∠HGK=∠GOS
∴△HGK∽△GOS,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案【题目】某工厂为了检验甲、乙两个车间生产的同一款产品的质量情况,进行了抽样调查,请补充完整.
收集数据 从甲、乙两个车间各随机抽取20个样品,进行了检测,检测结果(单位:mm)如下:
甲车间 | 168 | 175 | 180 | 185 | 172 | 189 | 185 | 182 | 185 | 174 |
192 | 180 | 185 | 178 | 173 | 185 | 169 | 187 | 176 | 180 | |
乙车间 | 186 | 180 | 189 | 183 | 176 | 173 | 178 | 167 | 180 | 175 |
178 | 182 | 180 | 179 | 185 | 180 | 184 | 182 | 180 | 183 |
整理、描述数据 按如下分段整理、描述这两组样本数据:
165.5-170.5 | 170.5-175.5 | 175.5-180.5 | 180.5-185.5 | 185.5-190.5 | 190.5-195.5 | |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 |
(说明:尺寸范围为176mm~190mm的产品为合格)
分析数据 两组样本数据的平均数、众数、中位数、方差如下表所示:
平均数 | 众数 | 中位数 | 方差 | |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
得出结论
(1)补全上列表格;
(2)若乙车间生产1000个该款产品,估计其中合格产品约有 个;
(3)可以推断出 车间生产的该款产品更好,理由为