题目内容
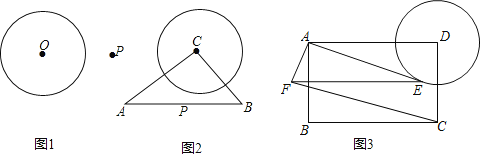
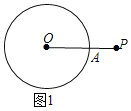
【题目】(1)如图1,A是⊙O上一动点,P是⊙O外一点,在图中作出PA最小时的点A.
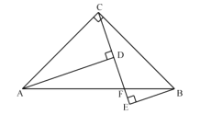
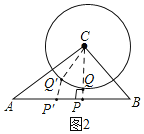
(2)如图2,Rt△ABC中,∠C=90°,AC=8,BC=6,以点C为圆心的⊙C的半径是3.6,Q是⊙C上一动点,在线段AB上确定点P的位置,使PQ的长最小,并求出其最小值.
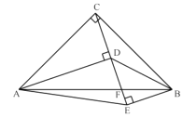
(3)如图3,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,∠EAF=90°,tan∠AEF=![]() ,试探究四边形ADCF的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
,试探究四边形ADCF的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
【答案】(1)作图见解析;(2)PQ长最短是1.2;(3)四边形ADCF面积最大值是![]() ,最小值是
,最小值是![]() .
.
【解析】
(1)连接线段OP交⊙C于A,点A即为所求;
(2)过C作CP⊥AB于Q,P,交⊙C于Q,这时PQ最短,根据勾股定理以及三角形的面积公式即可求出其最小值;
(3)△ACF的面积有最大和最小值,取AB的中点G,连接FG,DE,证明△FAG~△EAD,进而证明点F在以G为圆心1为半径的圆上运动,过G作GH⊥AC于H,交⊙G于F1,GH反向延长线交⊙G于F2,①当F在F1时,△ACF面积最小,分别求出△ACD的面积和△ACF的面积的最小值即可得出四边形ADCF的面积的最小值;②当F在F2时,四边形ADCF的面积有最大值,在⊙G上任取异于点F2的点P,作PM⊥AC于M,作GN⊥PM于N,利用矩形的判定与性质以及三角形的面积公式即可得出得出四边形ADCF的面积的最大值.
解:(1)连接线段OP交⊙C于A,点A即为所求,如图1所示;
(2)过C作CP⊥AB于Q,P,交⊙C于Q,这时PQ最短.
理由:分别在线段AB,⊙C上任取点P',点Q',连接P',Q',CQ',如图2,
由于CP⊥AB,根据垂线段最短,CP≤CQ'+P'Q',
∴CO+PQ≤CQ'+P'Q',
又∵CQ=CQ',
∴PQ<P'Q',即PQ最短.
在Rt△ABC中![]() ,
,![]() ,
,
∴![]() ,
,
∴PQ=CP﹣CQ=6.8﹣3.6=1.2,
∴![]() .
.
当P在点B左侧3.6米处时,PQ长最短是1.2.
(3)△ACF的面积有最大和最小值.
如图3,取AB的中点G,连接FG,DE.
∵∠EAF=90°,![]() ,
,
∴![]()
∵AB=6,AG=GB,
∴AC=GB=3,
又∵AD=9,
∴![]() ,
,
∴![]()
∵∠BAD=∠B=∠EAF=90°,
∴∠FAG=∠EAD,
∴△FAG~△EAD,
∴![]() ,
,
∵DE=3,
∴FG=1,
∴点F在以G为圆心1为半径的圆上运动,
连接AC,则△ACD的面积=![]() ,
,
过G作GH⊥AC于H,交⊙G于F1,GH反向延长线交⊙G于F2,
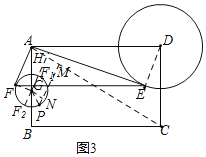
①当F在F1时,△ACF面积最小.理由:由(2)知,当F在F1时,F1H最短,这时△ACF的边AC上的高最小,所以△ACF面积有最小值,
在Rt△ABC中,![]()
∴![]() ,
,
在Rt△ACH中,![]() ,
,
∴![]() ,
,
∴△ACF面积有最小值是:![]() ;
;
∴四边形ADCF面积最小值是:![]() ;
;
②当F在F2时,F2H最大理由:在⊙G上任取异于点F2的点P,作PM⊥AC于M,作GN⊥PM于N,连接PG,则四边形GHMN是矩形,
∴GH=MN,
在Rt△GNP中,∠NGF2=90°,
∴PG>PN,
又∵F2G=PG,
∴F2G+GH>PN+MN,即F2H>PM,
∴F2H是△ACF的边AC上的最大高,
∴面积有最大值,
∵![]() ,
,
∴△ACF面积有最大值是![]() ;
;
∴四边形ADCF面积最大值是![]() ;
;
综上所述,四边形ADCF面积最大值是![]() ,最小值是
,最小值是![]() .
.

 口算能手系列答案
口算能手系列答案