Question

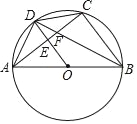
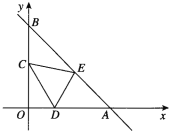
【题目】已知：如图，直线y＝－x＋12分别交x轴、y轴于A、B点，将△AOB折叠，使A点恰好落在OB的中点C处，折痕为DE．

(1)求AE的长及sin∠BEC的值；

(2)求△CDE的面积．

Answer 1

【答案】（1）5，sin∠BEC=；（2）

【解析】

（1）如图，作CF⊥BE于F点，由函数解析式可得点B，点A坐标，继而可得∠A=∠B=45°，再根据中点的定义以及等腰直角三角形的性质可得OC=BC=6，CF=BF=3，

设AE=CE=x，则EF=AB-BF-AE=12-3-x=9-x，在Rt△CEF中，利用勾股定理求出x的值即可求得答案；

（2）如图，过点E作EM⊥OA于点M，根据三角形面积公式则可得S△CDE=S△AED=AD×AE，设AD=y，则CD=y，OD=12-y，在Rt△OCD中，利用勾股定理求出y，继而可求得答案.

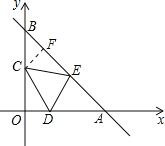
（1）如图，作CF⊥BE于F点，

由函数解析式可得点B（0，12），点A（12，0），∠A=∠B=45°，

又∵点C是OB中点，

∴OC=BC=6，CF=BF=3，

设AE=CE=x，则EF=AB-BF-AE=12-3-x=9-x，

在Rt△CEF中，CE2=CF2+EF2，即x2=（9-x）2+（3）2，

解得：x=5，

故可得sin∠BEC=，AE=5；

（2）如图，过点E作EM⊥OA于点M，

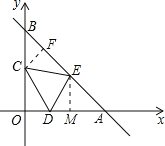
则S△CDE=S△AED=ADEM=AD×AEsin∠EAM=ADAE×sin45°=AD×AE，

设AD=y，则CD=y，OD=12-y，

在Rt△OCD中，OC2+OD2=CD2，即62+（12-y）2=y2，

解得：y=，即AD=，

故S△CDE=S△AED=AD×AE=．