Question

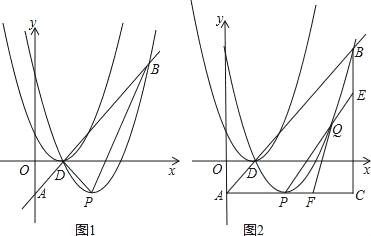
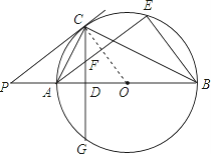
【题目】如图，AB为⊙O的直径，P是BA延长线上一点，CG是⊙O的弦∠PCA＝∠ABC，CG⊥AB，垂足为D

（1）求证：PC是⊙O的切线；

（2）求证：；

（3）过点A作AE∥PC交⊙O于点E，交CD于点F，连接BE，若sin∠P＝，CF＝5，求BE的长．

Answer 1

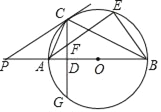
【答案】（1）见解析；（2）BE=12．

【解析】

（1）连接OC，由PC切⊙O于点C，得到OC⊥PC，于是得到∠PCA+∠OCA=90°，由AB为⊙O的直径，得到∠ABC+∠OAC=90°，由于OC=OA，证得∠OCA=∠OAC，于是得到结论；
（2）由AE∥PC，得到∠PCA=∠CAF根据垂径定理得到弧AC=弧AG，于是得到∠ACF=∠ABC，由于∠PCA=∠ABC，推出∠ACF=∠CAF，根据等腰三角形的性质得到CF=AF，在Rt△AFD中，AF=5，sin∠FAD=，求得FD=3，AD=4，CD=8，在Rt△OCD中，设OC=r，根据勾股定理得到方程r2=（r-4）2+82，解得r=10，得到AB=2r=20，由于AB为⊙O的直径，得到∠AEB=90°，在Rt△ABE中，由sin∠EAD=，得到＝，于是求得结论．

（1）证明：连接OC，

∵PC切⊙O于点C，

∴OC⊥PC，

∴∠PCO=90°，

∴∠PCA+∠OCA=90°，

∵AB为⊙O的直径，

∴∠ACB=90°，

∴∠ABC+∠OAC=90°，

∵OC=OA，

∴∠OCA=∠OAC，

∴∠PCA=∠ABC；

（2）解：∵AE∥PC，

∴∠PCA=∠CAF，

∵AB⊥CG，

∴弧AC=弧AG，

∴∠ACF=∠ABC，

∵∠PCA=∠ABC，

∴∠ACF=∠CAF，

∴CF=AF，

∵CF=5，

∴AF=5，

∵AE∥PC，

∴∠FAD=∠P，

∵sin∠P=，

∴sin∠FAD=，

在Rt△AFD中，AF=5，sin∠FAD=，

∴FD=3，AD=4，∴CD=8，

在Rt△OCD中，设OC=r，

∴r2=（r﹣4）2+82 ，

∴r=10，

∴AB=2r=20，

∵AB为⊙O的直径，

∴∠AEB=90°，在Rt△ABE中，

∵sin∠EAD=，∴，

∵AB=20，

∴BE=12．