题目内容
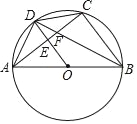
【题目】如图，AB是⊙O的直径，点C是圆上任意一点，点D是AC中点，OD交AC于点E，BD交AC于点F，若BF＝1.25DF，则tan∠ABD的值为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由△ADF∽△BDA，推出AD2=DFDB，由BF=1.25DF，可以假设DF=4m，则BF=5m，BD=9m，可得AD=6m，根据tan∠ABD=
计算即可解决问题．
∵
，
∴∠DAF=∠DBA，
∵∠ADF=∠ADB，
∴△ADF∽△BDA，
∴
，
∴AD2=DFDB，
∵BF=1.25DF，
∴可以假设DF=4m，则BF=5m，BD=9m，
∴AD2=36m2，
∵AD＞0，
∴AD=6m，
∵AB是直径，
∴∠ADB=90°，
∴tan∠ABD=
，
故选A．
练习册系列答案
阅读快车系列答案
相关题目
