题目内容
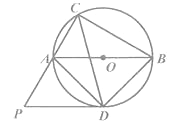
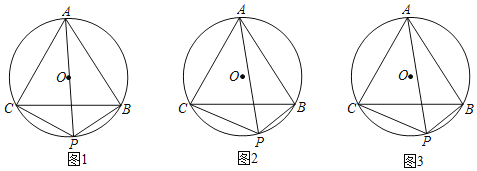
【题目】如图,△ABC是⊙O的内接正三角形,点P在劣弧BC上(不与点B,C重合).
(1)如图1,若PA是⊙O的直径,则PA______PB+PC(请填“>”,“=”或“<”)
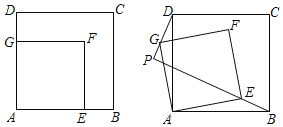
(2)如图2,若PA不是⊙O的直径,那么(1)中的结论是否仍成立?如果不成立,请说明理由:如果成立,请给出证明.
(3)如图3,若四边形ACPB的面积是16![]() .
.
①求PA的长;
②设y=S△PCB+![]() S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
【答案】(1)=;(2)结论仍然成立,理由见解析.(3)①PA=8,②PC=5,y的值最大,△ABC的外接圆的半径为![]() .
.
【解析】
(1)根据△ABC是等边三角形,⊙O是△ABC的外接圆,PA是直径,得PC=![]() PA,PB=
PA,PB=![]() PA;(2)根据等边三角形的性质和判定,可证△CBE≌△ABE(SAS),PC=AE,故PA=PE+AE=PB+PC;(3)①如图3中,作CM⊥PA于M,BN⊥PA于N.根据S四边形ACPB=S△PAC+S△PAB得16
PA;(2)根据等边三角形的性质和判定,可证△CBE≌△ABE(SAS),PC=AE,故PA=PE+AE=PB+PC;(3)①如图3中,作CM⊥PA于M,BN⊥PA于N.根据S四边形ACPB=S△PAC+S△PAB得16![]() =
=![]() PACM+
PACM+![]() PABN,根据三角函数得CM=PCsin60°,BN=PCsin60°,故16
PABN,根据三角函数得CM=PCsin60°,BN=PCsin60°,故16![]() =
=![]() PA(PB+PC),PA2=64;②设PC=x,则PB=8-x,
PA(PB+PC),PA2=64;②设PC=x,则PB=8-x,
由y=S△PCB+![]() S△PCA=
S△PCA=![]() PCPBsin60°+
PCPBsin60°+![]() 8PCsin60°,得y=
8PCsin60°,得y=![]() x(8-x)+
x(8-x)+![]() x=-
x=-![]() x2+
x2+![]() x=-
x=-![]() (x-5)2+
(x-5)2+![]() ,根据二次函数二次函数最值性质和勾股定理可求解.
,根据二次函数二次函数最值性质和勾股定理可求解.
解:(1)如图1中,
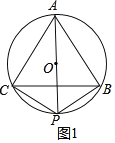
∵△ABC是等边三角形,⊙O是△ABC的外接圆,PA是直径,
∴PA平分∠BAC,∠ACP=∠ABP=90°,
∴∠PAC=∠PAB=![]() ×60°=30°,
×60°=30°,
∴PC=![]() PA,PB=
PA,PB=![]() PA,
PA,
∴PA=PB+PC.
故答案为=.
(2)结论仍然成立.
理由:如图2中,在PA上取一点E,使得PE=PB.
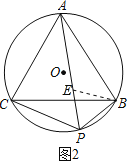
∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°,
∴∠APB=∠ACB=60°,
∵PE=PB,
∴△PBE是等边三角形,
∴∠PBE=∠ABC=60°,
∴∠ABE=∠CBP,
∵BC=BA,BP=BE,
∴△CBE≌△ABE(SAS),
∴PC=AE,
∴PA=PE+AE=PB+PC.
(3)①如图3中,作CM⊥PA于M,BN⊥PA于N.
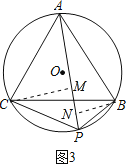
∵S四边形ACPB=S△PAC+S△PAB,
∴16![]() =
=![]() PACM+
PACM+![]() PABN,
PABN,
∵∠APC=∠ABC=60°,∠APB=∠ACB=60°,
∴CM=PCsin60°,BN=PCsin60°,
∴16![]() =
=![]() PA(PB+PC),
PA(PB+PC),
∵PB+PC=PA,
∴PA2=64,
∵PA>0,
∴PA=8.
②设PC=x,则PB=8-x,
∵y=S△PCB+![]() S△PCA=
S△PCA=![]() PCPBsin60°+
PCPBsin60°+![]() 8PCsin60°,
8PCsin60°,
∴y=![]() x(8-x)+
x(8-x)+![]() x=-
x=-![]() x2+
x2+![]() x=-
x=-![]() (x-5)2+
(x-5)2+![]() ,
,
∵-![]() <0,
<0,
∴x=5时,y有最大值,
∴PC=5,CM=![]() ,PM=
,PM=![]() ,AM=
,AM=![]() ,
,
在Rt△ACM中,AC=![]() =7,
=7,
∴△ABC的外接圆的半径为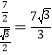 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案