Question

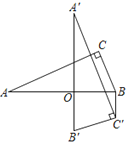
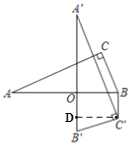
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝5，将△ABC绕AB上的点O顺时针旋转90°，得到△A'B'C'，连结BC'．若BC'∥A'B'，则OB的值为（ ）

A. B. 5C. D.

Answer 1

【答案】A

【解析】

过C′作C′D⊥A′B′于D，可得∠A′DC′=90°，由旋转性质可得∠BOD=90°，进而可证明AB//C′D，由BC′//A′B′，可证明四边形ODC′B是矩形，可得OB=C′D，由勾股定理可求出AB的长，利用面积公式求出C′D的长即可得答案.

过C′作C′D⊥A′B′于D，

∴∠A′DC′=90°，

∵将△ABC绕AB上的点O顺时针旋转90°，得到△A'B'C'，

∴∠BOD=90°，

∴AB//C′D，

∵BC′//A′B′，

∴四边形ODC′B是矩形，

∴OB=C′D，

∵∠C=90°，AC=12，BC=5，

∴AB==13，

∵S△A′B′C′=A′B′C′D=B′C′A′C′，

∴C′D===，

∴OB=C′D=，

故选A.