题目内容
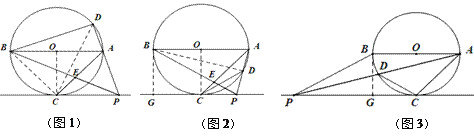
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

【答案】(1)45°;(2)见解析;(3)①∠ACD=15°;∠ACD=105°;∠ACD=60°;∠ACD=120°
②36或![]() .
.
【解析】试题分析:(1)易得△ABC是等腰直角三角形,从而∠BAC=∠CBA=45°;
(2)分当 B在PA的中垂线上,且P在右时;B在PA的中垂线上,且P在左;A在PB的中垂线上,且P在右时;A在PB的中垂线上,且P在左时四中情况求解;
(3)①先说明四边形OHEF是正方形,再利用△DOH∽△DFE求出EF的长,然后利用割补法求面积;②根据△EPC∽△EBA可求PC=4,根据△PDC∽△PCA可求PD PA=PC2=16,再根据S△ABP=S△ABC得到![]() ,利用勾股定理求出k2,然后利用三角形面积公式求解.
,利用勾股定理求出k2,然后利用三角形面积公式求解.
(1)解:(1)连接BC,
∵AB是直径,
∴∠ACB=90°.
∴△ABC是等腰直角三角形,
∴∠BAC=∠CBA=45°;
(2)解:∵![]() ,∴∠CDB=∠CDP=45°,CB= CA,
,∴∠CDB=∠CDP=45°,CB= CA,
∴CD平分∠BDP
又∵CD⊥BP,∴BE=EP,
即CD是PB的中垂线,
∴CP=CB= CA,
(3)① (Ⅰ)如图2,当 B在PA的中垂线上,且P在右时,∠ACD=15°;
(Ⅱ)如图3,当B在PA的中垂线上,且P在左,∠ACD=105°;
(Ⅲ)如图4,A在PB的中垂线上,且P在右时∠ACD=60°;
(Ⅳ)如图5,A在PB的中垂线上,且P在左时∠ACD=120°
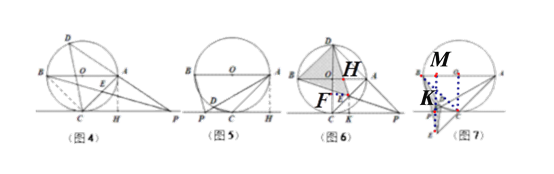
②(Ⅰ)如图6,![]() ,
,![]()
![]()
![]()
![]() .
.
(Ⅱ)如图7,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设BD=9k,PD=2k,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.