题目内容
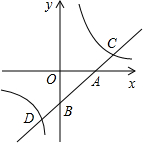
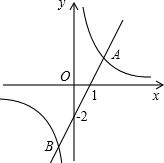
如图,已知直线y=
x与双曲线y=
(k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y=
(k>0)上一点C的纵坐标为8,求△AOC的面积.

| 1 |
| 2 |
| k |
| x |
(1)求k的值;
(2)若双曲线y=
| k |
| x |

(1)∵点A横坐标为4,
∴当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y=
x与双曲线y=
(k>0)的交点,
∴k=4×2=8.(3分)
(2)如图,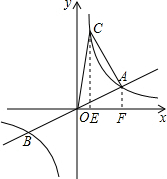
过点C、A分别作x轴的垂线,垂足为E、F,
∵点C在双曲线y=
上,当y=8时,x=1.
∴点C的坐标为(1,8).
∵点C、A都在双曲线y=
上,
∴S△COE=S△AOF=4.
∴S△COE+S梯形CEFA=S△COA+S△AOF.
∴S△COA=S梯形CEFA.(6分)
∵S梯形CEFA=
×(2+8)×3=15,
∴S△COA=15.(8分)
∴当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y=
| 1 |
| 2 |
| k |
| x |
∴k=4×2=8.(3分)
(2)如图,

过点C、A分别作x轴的垂线,垂足为E、F,
∵点C在双曲线y=
| 8 |
| x |
∴点C的坐标为(1,8).
∵点C、A都在双曲线y=
| 8 |
| x |
∴S△COE=S△AOF=4.
∴S△COE+S梯形CEFA=S△COA+S△AOF.
∴S△COA=S梯形CEFA.(6分)
∵S梯形CEFA=
| 1 |
| 2 |
∴S△COA=15.(8分)

练习册系列答案
相关题目