Question

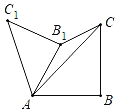
【题目】我们规定：如果一个三角形有一边上的中线等于这条边的一半，那么称这个三角形为“智慧三角形”．

理解：

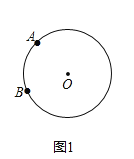
（1）如图1，已知A、B是⊙O上两点，请在圆上找出满足条件的点C，使△ABC为“智慧三角形”（画出点C的位置，保留作图痕迹）；

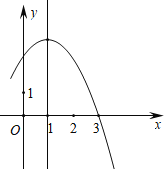
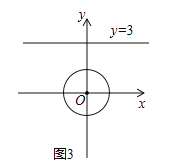
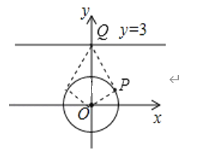
（2）如图3，在平面直角坐标系xOy中，⊙O的半径为1，点Q是直线y＝3上的一点，若在⊙O上存在一点P，使得△OPQ为“智慧三角形”，当其面积取得最小值时，直接写出此时PQ的长和点Q的坐标

Answer 1

【答案】（1）见解析；（2），Q(0,3)

【解析】

（1）连结BO并且延长交圆于C1，连结AO并且延长交圆于C2，即可求解；

（2）根据“智慧三角形”的定义可得△OPQ为直角三角形，根据题意可得一条直角边为1，当斜边最短时，另一条直角边最短，则面积取得最小值，由垂线段最短可得斜边最短为3，从而得到点Q坐标，再根据勾股定理可求另一条直角边即PQ长．

解：（1）如图所示，过直径做△ABC即可；

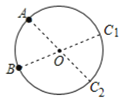
（2）如图所示：

由“智慧三角形”的定义可得△OPQ为直角三角形，

根据题意可得一条直角边OP＝1，

∴PQ最小时，△POQ的面积最小，

根据勾股定理可知，当斜边OQ最短时，PQ最小，面积取得最小值，

由垂线段最短可得斜边最短为3，即OQ=3，

∴Q（0，3），

由勾股定理可得PQ＝＝，

∴当面积取得最小值时，点Q的坐标为(0，3)，PQ的长为.