题目内容
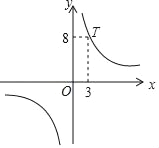
【题目】如果把函数y＝x2（x≤2）的图象和函数y＝
的图象组成一个图象，并称作图象E，那么直线y＝3与图象E的交点有_____个；若直线y＝m（m为常数）与图象E有三个不同的交点，则常数m的取值范围是_____．
【答案】2， 0＜m＜2．
【解析】
在同一直角坐标系中，画出函数y=x2（x≤2）和函数y=
(x＞2)的图象，根据函数图象即可得到直线y=3与图象E的交点个数以及常数m的取值范围．
解：在同一直角坐标系中，画出函数y=x2（x≤2）和函数y= (x＞2)的图象，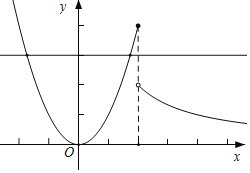
由图可得，直线y=3与图象E的交点有2个，
∵直线y=m（m为常数）与图象E有三个不同的交点，
∴直线y=m在直线y=2的下方，且在x轴的上方，
∴常数m的取值范围是0＜m＜2，
故答案为：2，0＜m＜2．
练习册系列答案
相关题目
【题目】当前，“校园ipad现象已经受到社会的广泛关注，某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查．小文将调查数据作出如下不完整的整理：
频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |
（1）请求出共调查了多少人；并把小文整理的图表补充完整；
（2）小丽要将调查数据绘制成扇形统计图，则扇形图中“赞成”的圆心角是多少度？
（3）若该校有3000名学生，请您估计该校持“反对”态度的学生人数．
