题目内容
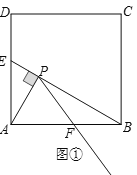
【题目】如图,正方形ABCD的边长是6,点E、F分别是边AD、AB的点,AP⊥BE于点P.
(1)如图①,当AE=2![]() 且AF=BF时,若点T是射线PF上的一个动点(点T不与点P重合),当△ABT是直角三角形时,求AT的长.
且AF=BF时,若点T是射线PF上的一个动点(点T不与点P重合),当△ABT是直角三角形时,求AT的长.
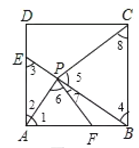
(2)如图②,当AE=AF时,连结CP,判断CP与PF的位置关系,并加以证明.

【答案】(1)AT=3![]() 或3
或3![]() ;(2)CP⊥PF,证明见解析.
;(2)CP⊥PF,证明见解析.
【解析】
(1)解Rt△BAE,求出∠ABE=30°,然后分三种情况进行讨论:①当点T在AB的上方,∠ATB=90°时,点T和点P重合,不符合题意;②当点T在AB的下方,∠ATB=90°时,根据直角三角形斜边上的中线等于斜边的一半可得TF=BF=AF=3,而∠BFT=60°,那么△FTB是等边三角形,TB=3,再根据勾股定理求出AT; ③当点T在AB的下方,∠ABT=90°时,解直角三角形求出BT,然后在Rt△ATB中利用勾股定理求出AT;
(2)先证明∠1=∠3=∠4,由tan∠1=![]() ,tan∠3=
,tan∠3=![]() ,得出
,得出![]() ,等量代换得到
,等量代换得到![]() ,然后可证明△PBC∽△PAF,得出∠5=∠6,进而可得∠5+∠7=90°,即∠CPF=90°,那么CP⊥PF.
,然后可证明△PBC∽△PAF,得出∠5=∠6,进而可得∠5+∠7=90°,即∠CPF=90°,那么CP⊥PF.
解:(1)在正方形ABCD中,可得∠DAB=90°,
∵在Rt△BAE中,tan∠ABE=![]() ,
,
∴∠ABE=30°,
点T是射线PF上的一个动点,当△ABT为直角三角形时,分三种情况:
①当点T在AB的上方,∠ATB=90°,
此时点T和点P重合,与题意不符;
②当点T在AB的下方,∠ATB=90°,
如图所示,在Rt△APB中,由AF=BF,可得:AF=BF=PF=3,
∴∠BPF=∠FBP=30°,
∴∠BFT=60°,
在Rt△ATB中,TF=BF=AF=3,
∴△FTB是等边三角形,
∴TB=3,AT=![]() ;
;
③当点T在AB的下方,∠ABT=90°时,
如图所示,在Rt△FBT中,∠BFT=60°,BF=3,BT=BFtan60°=![]() ,
,
在Rt△ATB中:AT=![]() ,
,
综上所述:当△ABT为直角三角形时,AT的长为![]() 或
或![]() ;
;
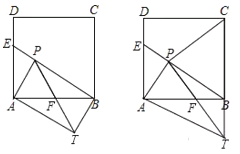
(2)CP⊥PF,
证明:如图所示,∵四边形ABCD是正方形,
∴AB=AD=BC,AD∥BC,∠DAB=90°,
∴∠3=∠4,
∵在Rt△EAB中,AP⊥BE,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
∴∠1=∠3=∠4,
∵tan∠1=![]() ,tan∠3=
,tan∠3=![]() ,
,
∴![]() ,
,
∵AE=AF,AB=BC,
∴![]() ,
,
∴△PBC∽△PAF,
∴∠5=∠6.
∵∠6+∠7=90°,
∴∠5+∠7=90°,即∠CPF=90°,
∴CP⊥PF.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案