题目内容
【题目】已知抛物线y＝3x2+bx+c与直线y＝﹣1只有一个公共点M，与平行于x轴的直线l交此抛物线A，B两点若AB=4，则点M到直线l的距离为（ ）
A.11B.12C.
D.13
【答案】B
【解析】
根据题意可知，抛物线的顶点M（
），则抛物线解析式为：
，由AB=4，利用抛物线的对称性，得点A的横坐标为
，代入解析式，求出纵坐标，然后求出点M到直线l的距离.
解：∵抛物线y＝3x2+bx+c与直线y＝﹣1只有一个公共点M，
∴点M为抛物线的顶点，其坐标为：（
，
），
则抛物线解析式为：，
∵抛物线与平行于x轴的直线l交此抛物线A，B两点，且AB=4，
∴点A的横坐标为：，点B的横坐标为：
，
把
代入抛物线，得：
，
∴直线l为：
，
∴点M到直线l的距离为：11﹣（﹣1）=12；
故选择：B.
练习册系列答案
相关题目
【题目】小明对函数y＝﹣|x2﹣4|的图象和性质进行了探究，其探究过程中的列表如下：
x | … | -3 | ﹣2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | m | 0 | -3 | n | -3 | 0 | -5 | … |
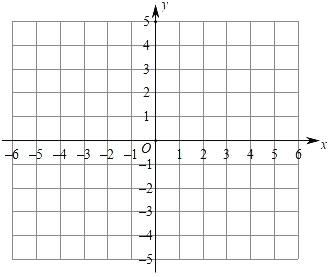
（1）求表中m，n的值；
（2）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了该函数的图象；
（3）观察函数图象，写出一条函数的性质；
（4）结合你所画的函数图象，直接写出不等式﹣|x2﹣4|＞x﹣2的解集．