题目内容
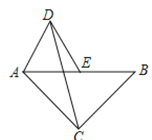
【题目】如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8,点E是AB的中点,以AE为边作等边△ADE(点D与点C分别在AB异侧),连接CD,则△ACD的面积是_________.
【答案】![]()
【解析】
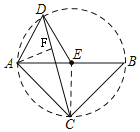
连接CE,根据圆的定义,证明D、A、C、B四点共圆,可得∠ADC=∠ABC=45°,作AF⊥CD于F,构建等腰直角三角形ADF和含30°角的直角三角形AFC,可以求得AF、DF、CF的长,利用三角形面积公式可得结论.
解:连接CE,
∵∠ACB=90°,E为AB的中点,
∴CE=AE=BE,
∵△ADE是等边三角形,
∴DE=AE,
∴DE=AE=CE=BE,
∴D、A、C、B在以点E为圆心的圆上,作⊙E,
∴∠ADC=∠ABC=45°,
过A作AF⊥CD于F,
∴△ADF是等腰直角三角形,
∵AD=AE=![]() AB=4,
AB=4,
∴AF=DF=![]() ,
,
∵∠CAF=∠DAB+∠BAC-∠DAF=60°+45°-45°=60°,
∴∠ACF=30°,
∴AC=2AF![]() ,
,
由勾股定理得:CF=![]() ,
,
∴S△ADC=![]() ,
,
故答案为:4+4![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目