题目内容
【题目】(2014河南22题)
(1)问题发现
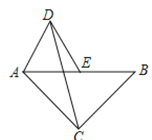
如图①,![]() 和
和![]() 均为等边三角形,点A、D、E在同一条直线上,连接BE;
均为等边三角形,点A、D、E在同一条直线上,连接BE;
填空:
①![]() 的度数为__________;
的度数为__________;
②线段AD、BE之间的数量关系为__________.
(2)拓展探究
如图②,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点A、D、E在同一条直线上,CM为
,点A、D、E在同一条直线上,CM为![]() 中DE边上的高,连接BE.请判断
中DE边上的高,连接BE.请判断![]() 的度数及线段CM、AE、BE之间的数量关系,并说明理由;
的度数及线段CM、AE、BE之间的数量关系,并说明理由;
(3)解决问题
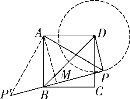
如图③,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点A到BP的距离.
,请直接写出点A到BP的距离.
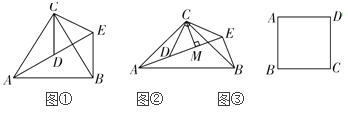
图① 图② 图③
【答案】(1)①60°;②![]() ;(2)①
;(2)①![]() ;②
;②![]() ,详见解析;(3)
,详见解析;(3)![]() 或
或![]()
【解析】
(1)[思维教练]由![]() 和
和![]() 均为等边三角形可证
均为等边三角形可证![]() ,即可知AD与BE之间的数量关系,再由等边三角形和全等三角形的性质求得
,即可知AD与BE之间的数量关系,再由等边三角形和全等三角形的性质求得![]() 的度数;
的度数;
[自主作答]
(2)[思维教练]由![]() 和
和![]() 均为等腰直角三角形可证
均为等腰直角三角形可证![]() ,即可知
,即可知![]() ,
,![]() ,再由
,再由![]() 是等腰直角三角形,可知
是等腰直角三角形,可知![]() ,从而证明结论.
,从而证明结论.
[自主作答]
(3)[思维教练]根据题意可作以点D为圆心,PD长为半径的圆,再过点B作圆的切线,分两种情况:第一种情况过点A作![]() 于点M,过点A作AP的垂线,交BP于点
于点M,过点A作AP的垂线,交BP于点![]() ,易证
,易证![]() ,即可得
,即可得![]() ,由勾股定理可求PB的长,从而求得
,由勾股定理可求PB的长,从而求得![]() 的长,再由
的长,再由![]() 是等腰直角三角形可得
是等腰直角三角形可得![]() ,即可求解;第二种情况与第一种情况相同解法可得
,即可求解;第二种情况与第一种情况相同解法可得![]() ,运用勾股定理和全等三角形求出
,运用勾股定理和全等三角形求出![]() 与PB的长即可求解.
与PB的长即可求解.
解:(1)① 60°;②![]() ;
;
[解法提示]①![]() 和
和![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;②由①得
;②由①得![]() ,
,![]() .
.
(2)①![]() ;②
;②![]() .理由如下:
.理由如下:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .在等腰直角三角形
.在等腰直角三角形![]() 中,
中,![]() 为斜边
为斜边![]() 上的高,
上的高,![]() ,
,![]() ,
,![]() ;
;
(3) ![]() 或
或![]() .
.
[解法提示]![]() ,
,![]() ,
,![]() 是以点
是以点![]() 为圆心,以1为半径的
为圆心,以1为半径的![]() 的切线,点
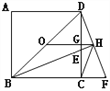
的切线,点![]() 为切点.第一种情况:如解图①,过
为切点.第一种情况:如解图①,过![]() 点作
点作![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,易证
,易证![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,第二种情况:如解图②,可得
,第二种情况:如解图②,可得![]() .
.
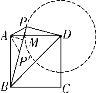
图① 图②

【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.