题目内容
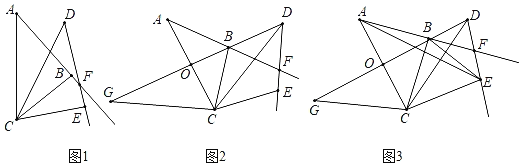
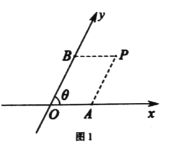
【题目】阅读材料并解答下列问题:如图1,把平面内一条数轴![]() 绕原点
绕原点![]() 逆时针旋转角
逆时针旋转角![]() 得到另一条数轴
得到另一条数轴![]() 轴和
轴和![]() 轴构成一个平面斜坐标系
轴构成一个平面斜坐标系![]()
规定:过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,若点
,若点![]() 在
在![]() 轴对应的实数为
轴对应的实数为![]() ,点
,点![]() 在
在![]() 轴对应的实数为
轴对应的实数为![]() ,则称有序实数对
,则称有序实数对![]() 为点
为点![]() 在平面斜坐标系
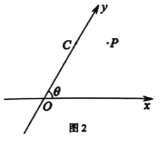
在平面斜坐标系![]() 中的斜坐标.如图2,在平面斜坐标系
中的斜坐标.如图2,在平面斜坐标系![]() 中,已知
中,已知![]() ,点
,点![]() 的斜坐标是
的斜坐标是![]() ,点
,点![]() 的斜坐标是
的斜坐标是![]()
(1)连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() (点
(点![]() 与点
与点![]() 对应),求点
对应),求点![]() 的斜坐标;
的斜坐标;
(3)若点![]() 是直线
是直线![]() 上一动点,在斜坐标系
上一动点,在斜坐标系![]() 确定的平面内以点
确定的平面内以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ,当⊙
,当⊙![]() 与
与![]() 轴相切时,求点
轴相切时,求点![]() 的斜坐标,
的斜坐标,
【答案】(1)![]() ;(2)点
;(2)点![]() 的斜坐标为(9,
的斜坐标为(9,![]() );(3)点D的斜坐标为:(
);(3)点D的斜坐标为:(![]() ,3)或(6,12).
,3)或(6,12).
【解析】
(1)过点P作PC⊥OA,垂足为C,由平行线的性质,得∠PAC=![]() ,由AP=6,则AC=3,
,由AP=6,则AC=3,![]() ,再利用勾股定理,即可求出OP的长度;
,再利用勾股定理,即可求出OP的长度;
(2)根据题意,过点Q作QE∥OC,QF∥OB,连接BQ,由旋转的性质,得到OP=OQ,∠COP=∠BOQ,则△COP≌△BOQ,则BQ=CP=3,∠OCP=∠OBQ=120°,然后得到△BEQ是等边三角形,则BE=EQ=BQ=3,则OE=9,OF=3,即可得到点Q的斜坐标;
(3)根据题意,可分为两种情况进行①当OP和CM恰好是平行四边形OMPC的对角线时,此时点D是对角线的交点,求出点D的坐标即可;②取OJ=JN=CJ,构造直角三角形OCN,作∠CJN的角平分线,与直线OP相交与点D,然后由所学的性质,求出点D的坐标即可.
解:(1)如图,过点P作PC⊥OA,垂足为C,连接OP,
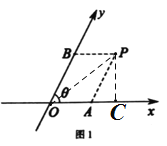
∵AP∥OB,
∴∠PAC=![]() ,
,
∵PC⊥OA,
∴∠PCA=90°,
∵点![]() 的斜坐标是
的斜坐标是![]() ,
,
∴OA=3,AP=6,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在Rt△OCP中,由勾股定理,得
![]() ;
;
(2)根据题意,过点Q作QE∥OC,QF∥OB,连接BQ,如图:
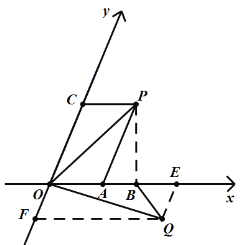
由旋转的性质,得OP=OQ,∠POQ=60°,
∵∠COP+∠POA=∠POA+∠BOQ=60°,
∴∠COP=∠BOQ,
∵OB=OC=6,
∴△COP≌△BOQ(SAS);
∴CP=BQ=3,∠OCP=∠OBQ=120°,
∴∠EBQ=60°,
∵EQ∥OC,
∴∠BEQ=60°,
∴△BEQ是等边三角形,
∴BE=EQ=BQ=3,
∴OE=6+3=9,OF=EQ=3,
∵点Q在第四象限,
∴点![]() 的斜坐标为(9,
的斜坐标为(9,![]() );
);
(3)①取OM=PC=3,则四边形OMPC是平行四边形,连接OP、CM,交点为D,如图:
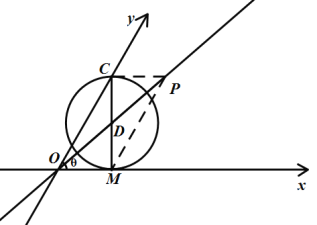
由平行四边形的性质,得CD=DM,OD=PD,
∴点D为OP的中点,
∵点P的坐标为(3,6),
∴点D的坐标为(![]() ,3);
,3);
②取OJ=JN=CJ,则△OCN是直角三角形,
∵∠COJ=60°,
∴△OCJ是等边三角形,
∴∠CJN=120°,
作∠CJN的角平分线,与直线OP相交于点D,作DN⊥x轴,连接CD,如图:
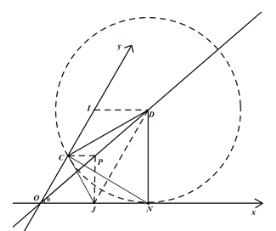
∵CJ=JN,∠CJD=∠NJD,JP=JP,
∴△CJD≌△NJD(SAS),
∴∠JCD=∠JND=90°,
则由角平分线的性质定理,得CD=ND;
过点D作DI∥x轴,连接DJ,
∵∠DJN=∠COJ=60°,
∴OI∥JD,
∴四边形OJDI是平行四边形,
∴ID=OJ=JN=OC=6,
在Rt△JDN中,∠JDN=30°,
∴JD=2JN=12;
∴点D的斜坐标为(6,12);
综合上述,点D的斜坐标为:(![]() ,3)或(6,12).
,3)或(6,12).

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案