题目内容
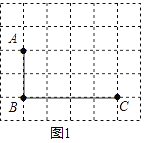
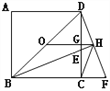
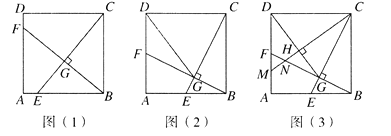
【题目】如图(1),在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作![]() 于点G,交AD于点F.
于点G,交AD于点F.
(1)求证:![]() ;
;
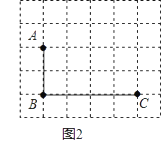
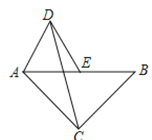
(2)如图(2),当点E运动到AB的中点时,连接DG,求证:![]() ;
;
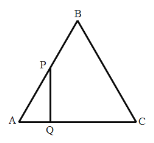
(3)如图(3),在(2)的条件下,过点C作![]() 于点H,分别交AD,BF于点M,N,求证:
于点H,分别交AD,BF于点M,N,求证:![]() .
.
【答案】(1)详见解析;(2)详见解析;(3)详见解析
【解析】
(1)先判断出∠GCB+∠CBG=90,再由四边形ABCD是正方形,得出∠CBE=90°=∠A,BC=AB,即可得出结论;
(2)取BC中点P,连接PD交CG于Q,先证平行四边形PBFD,进而可证PD是CG的垂直平分线,由此可得结论;
(3)先证![]() 得
得![]() ,再证
,再证![]() 得
得![]() ,继续证得
,继续证得![]() 得
得![]() 进而可得结论.
进而可得结论.
证明:(1)∵BF⊥CE,
∴∠CGB=90°,
∴∠GCB+∠CBG=90,
∵四边形ABCD是正方形,
∴∠CBE=90°=∠A,BC=AB,
∴∠FBA+∠CBG=90,
∴∠GCB=∠FBA,
∴△ABF≌△BCE(ASA);
(2)如图,取BC中点P,连接PD交CG于Q,
∵F是AD中点
∴![]() ,
,![]()
∴![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴Q是CG中点,
又![]() ,
,
∴![]() ,
,
∴PD是CG的垂直平分线,
∴![]() ,
,
(3)∵E是AB中点,P是BC中点,
∴![]() ,
,
又∵![]() ,
,![]()
∴![]() ,
,
由(2)知:![]()
∴![]()
又∵![]() ,
,![]() ,
,
∴![]()
∴![]()
又∵![]()
∴![]()
又∵在![]() 中,
中,![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]() .
.


练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目