Question

【题目】如图，，点、分别在、上，连接，、的平分线交于点，、的平分线交于点．

求证：四边形是矩形．

小明在完成的证明后继续进行了探索，过点作，分别交、于点、，过点作，分别交、于点、，得到四边形．此时，他猜想四边形是菱形．请在下列框图中补全他的证明思路．

小明的证明思路：由，，易证，四边形是平行四边形．要证□是菱形，只要证．由已知条件________，，可证，故只要证，即证，易证________，________，故只要证，易证，，________，故得，即可得证．

Answer 1

【答案】平分

【解析】

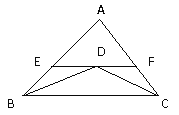
(1)由AB∥CD可得∠AEF=∠DFE，∠BEF=∠CFE，又由EG、FG、EH、FH均为角平分线可得DG∥FH，EH∥GF，且∠EGF=∠EHF=90°，故可得四边形EGFH为矩形；

(2)利用MN∥EF及FG是角平分线可证△NGF为等腰三角形，得NG=NF；再通过证明△MGE≌△QHF得MG=QF，从而得到NM=NQ进而证明四边形是菱形．

（1）证明：∵EH平分∠BEF，
∴∠FEH=∠BEF，
∵FH平分∠DFE，
∴∠EFH=∠DFE，
∵AB∥CD，
∴∠BEF+∠DFE=180°，
∴∠FEH+∠EFH=（∠BEF+∠DFE）=×180°=90°，
∵∠FEH+∠EFH+∠EHF=180°，
∴∠EHF=180°-（∠FEH+∠EFH）=180°-90°=90°，
同理可得：∠EGF=90°，
∵EG平分∠AEF，
∴∠EFG=∠AEF，
∵EH平分∠BEF，
∴∠FEH=∠BEF，
∵点A、E、B在同一条直线上，
∴∠AEB=180°，
即∠AEF+∠BEF=180°，
∴∠FEG+∠FEH=（∠AEF+∠BEF）=×180°=90°，
即∠GEH=90°
∴四边形EGFH是矩形；
（2） 答案不唯一：
由AB∥CD，MN∥EF，PQ∥EF，易证四边形MNQP是平行四边形，
要证MNQP是菱形，只要证MN=NQ，由已知条件：FG平分∠CFE，MN∥EF，
故只要证GM=FQ，即证△MGE≌△QFH，易证 GE=FH、∠GME=∠FQH．
故只要证∠MGE=∠QFH，易证∠MGE=∠GEF，∠QFH=∠EFH，∠GEF=∠EFH，即可得证；
故答案为：FG平分∠CFE，GE=FH、∠GME=∠FQH，∠GEF=∠EFH．