Question

【题目】如图，在锐角ΔABC中，已知AB=AC,D为底边BC上的一点，E为线段AD上的一点，且∠BED=∠BAC=2∠DEC，连接CE.

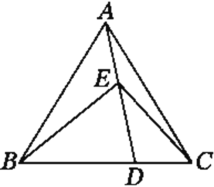
（1）求证：∠ABE=∠DAC

（2）若∠BAC=60°，试判断BD与CD有怎样的数量关系，并证明你的结论；

Answer 1

【答案】（1）见解析；（2）BD=2CD，理由见解析.

【解析】

（1）根据∠BED=∠BAE+∠ABE，∠BAC=∠BAE+∠DAC，且有∠BED=∠BAC，通过计算即可证得结论；
（2）在AD上取一点F，使得AF=BE，连接CF．过点C作CH∥BE，交直线AD于H点，证明△ACF≌△BAE（SAS），得出AE=CF，∠AEB=∠CFA，证出CF=CH，CF=EF，得出BE=2CH，由平行线分线段成比例定理得出BE：CH=BD：CD=2，即可得出结论．

（1）证明：

∵∠BED=∠BAE+∠ABE，∠BAC=∠BAE+∠DAC，

又∵∠BED =∠BAC，
∴∠BAE+∠ABE =∠BAE+∠DAC，
∴∠ABE=∠DAC；
（2）解：BD=2CD，理由如下：
如图，在AD上取一点F，使得AF=BE，连接CF．过点C作CH∥BE，交直线AD于H点．

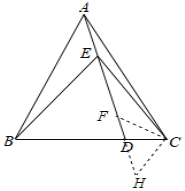
在△ACF和△BAE中，

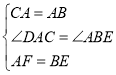
∴△ACF≌△BAE（SAS），
∴AE=CF，∠AEB=∠CFA，
∵∠AEB+∠BED=∠CFA+∠CFD=180°，
∴∠BED=∠CFD，
∵CH∥BE，
∴∠BED=∠CHD=∠CFD，
∴CF=CH，
∵∠BED=2∠DEC，∠CFD=∠DEC+∠ECF，

∴∠DEC=∠ECF，
∴CF=EF=AE，
∴BE=AF=2CH，
∵CH∥BE，
∴BE：CH=BD：CD=2，
即BD=2CD．