题目内容
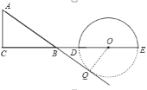
【题目】如图,形如量角器的半圆![]() 的直径
的直径![]() ,形如三角板的
,形如三角板的![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 以
以![]() 的速度从左向右运动,在运动过程中,点
的速度从左向右运动,在运动过程中,点![]() 、
、![]() 始终在直线
始终在直线![]() 上,设运动时间为
上,设运动时间为![]() ,当
,当![]() 时,半圆
时,半圆![]() 在
在![]() 的左侧,
的左侧,![]() .
.
![]() 当
当![]() 时,点
时,点![]() 在半圆
在半圆![]() ________,当
________,当![]() 时,点
时,点![]() 在半圆
在半圆![]() ________;
________;
![]() 当
当![]() 为何值时,
为何值时,![]() 的边
的边![]() 与半圆
与半圆![]() 相切?
相切?
![]() 当
当![]() 为何值时,
为何值时,![]() 的边
的边![]() 与半圆
与半圆![]() 相切?
相切?

【答案】(1)外,外;(2)2或14;(3)8或32.
【解析】
(1)计算出AC的长度,与半圆O的半径比较即可;(2)分情况画出图形,根据直线与圆相切的性质、特殊角的三角函数值求出点O运动的距离,进而求出时间t;(3)分情况画出图形,根据直线与圆相切的性质、特殊角的三角函数值求出点O运动的距离,进而求出时间t.
(1)AC=BC·tan30°=12×![]() =4
=4![]() >6,
>6,
∴t无论为何值,点A始终在半圆O外,
∴当t=0(s)时,点A在半圆O外,当t=8(s)时,点A在半圆O外;
(2)①如图,半圆O位于AC左侧时,
OC=6cm,t=(8﹣6)÷1=2(s);

②如图,半圆O位于AC右侧时,
OC=6cm,t=(8+6)÷1=14(s);

∴当t=2或14时,△ABC的边AC与半圆O相切;
(3)①如图,半圆O与AB相切于点F,连接OF,
∴OF⊥AB,
∵OF=6cm,∠ABC=30°,
∴BO=![]() =12cm,
=12cm,
∴点O与点C重合,
∴t=8÷1=8(s);

②如图,半圆O与AB的延长线相切于点Q,连接OQ,
∵∠OBQ=∠ABC=30°,OQ=6cm,
∴BO=![]() =12cm,
=12cm,
∴t=(12+12+8)÷1=32(s).
∴当t=8或32时,△ABC的边AB与半圆O相切;

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】保险公司车保险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:

(1)样本中,保费高于基本保费的人数为__________名;
(2)已知该险种的基本保费a为6 000元,估计1名续保人本年度的平均保费.







