题目内容
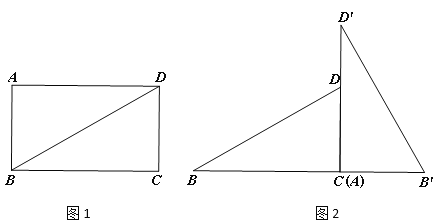
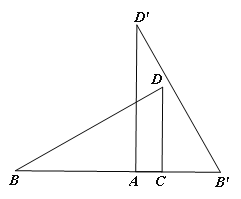
【题目】如图,已知矩形ABCD的对角线交于点E,将△DCB沿CD翻折得到△DCF.
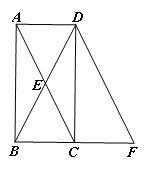
(1)求证:四边形ACFD是平行四边形;
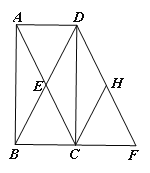
(2)点H为DF的中点,连结CH,若AB=4,BC=2,求四边形ECHD的面积.
【答案】(1)见解析;(2)4
【解析】
(1)由矩形的性质得到AD∥BC,根据折叠的性质得到BC=CF,根据平行四边形的判定定理即可得到结论;
(2)根据三角形的面积公式得到S△BCD=S△FCD=![]() ×2×4=4,由矩形的性质得到E为BD中点,根据三角形的面积公式即可得到结论.
×2×4=4,由矩形的性质得到E为BD中点,根据三角形的面积公式即可得到结论.
(1)证明:
∵四边形ABCD为矩形,
∴AD∥BC
由翻折可知:BC=CF
∴AD∥CF
∴四边形ACFD为平行四边形
(2)解:∵AB=4,BC=CF=2
又∵DC⊥BF
∴S△BCD=S△FCD=![]() =4
=4
∴四边形ABCD为矩形
∴E为BD中点
∴S△CED=![]() S△BCD=2
S△BCD=2
∵H为DF的中点
∴S△CDH=![]() S△DCF=2
S△DCF=2
∴S四边形ECHD=S△CED+S△DHC=2+2=4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目