题目内容
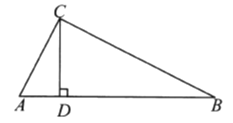
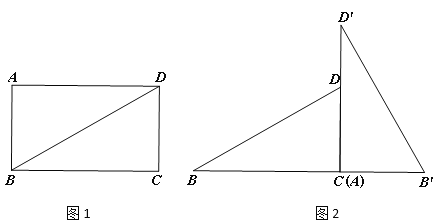
【题目】如图1,矩形ABCD,AB=4,BC=![]() .
.
(1)直接写出:∠ABD=______度;
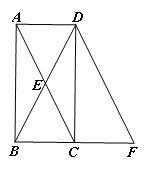
(2)将矩形ABCD沿BD剪开得到两个三角形,按图2摆放:点A与点C重合,CD落在AD′上,直接写出BD与B′D′的关系:_____;
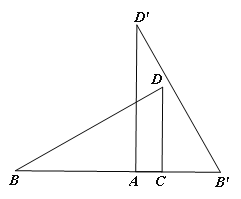
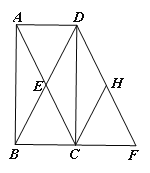
(3)在图2的基础上将△AB′D′向左平移,点B′与B重合停止,设AC=x,两个三角形重合部分的封闭图形的周长为y,请用x表示y:____.
【答案】60 BD=B′D′,BD⊥B′D′ 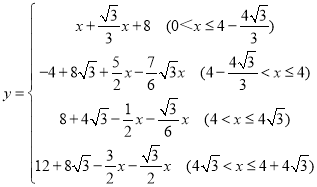
【解析】
(1)解直角三角形即可解决问题.
(2)结论:BD⊥B′D′,BD=B′D′.利用“8字型”证明∠DHD′=∠BAD=90°即可.
(3)分四种情形①如图3-1中,当0<x≤![]() 时,重叠部分是四边形ACDH.②如图3-2中,当
时,重叠部分是四边形ACDH.②如图3-2中,当![]() <x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当
<x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当![]() <x≤
<x≤![]() 时,重叠部分是五边形ACMNH.如图3-4中,当
时,重叠部分是五边形ACMNH.如图3-4中,当![]() <x<4+
<x<4+![]() 时,重叠部分是△BB′H.分别求解即可.
时,重叠部分是△BB′H.分别求解即可.
解:(1)如图1中,
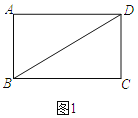
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=![]() ,
,
∴tan∠ABD=![]() ,
,
∴∠ABD=60°,
故答案为:60.
(2)结论:BD⊥B′D′,BD=B′D′.
理由:如图2中,延长BD交D′B′于H.
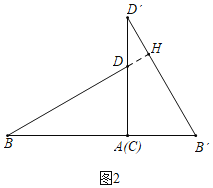
∵∠B=∠D′,∠BDA=∠HDD′,
∴∠BAD=∠DHD′=90°,
∴BD⊥B′D′.
∵BD与B′D′为矩形的对角线,则BD=B′D′;
故答案为:BD=B′D′,BD⊥B′D′.
(3)①如图3-1中,当0<x≤![]() 时,重叠部分是四边形ACDH,
时,重叠部分是四边形ACDH,
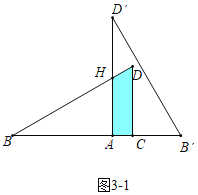
由题意:AB=![]() ,AH=
,AH=![]() AB=
AB=![]() ,
,
∵AH∥CD,
∴![]() ,
,
∴![]() ,
,
∴BH=![]() ,
,
∴DH=8-(![]() )=
)=![]() ,
,
y=x+4+![]()
=x+4+4![]()
=![]() ;
;
②如图3-2中,当![]() <x≤4时,重叠部分是五边形ACMNH.
<x≤4时,重叠部分是五边形ACMNH.
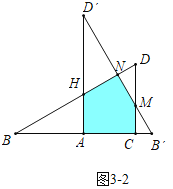
![]()
=![]()
=![]() ;
;
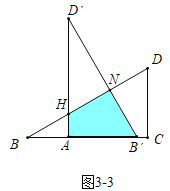
③如图3-3中,当4<x≤![]() 时,重叠部分是四边形AB′NH.
时,重叠部分是四边形AB′NH.
![]()
=![]()
=![]() ;
;
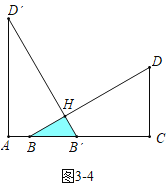
④如图3-4中,当![]() 时,重叠部分是△BB′H.
时,重叠部分是△BB′H.
![]()
![]()
![]() ;
;
故答案为: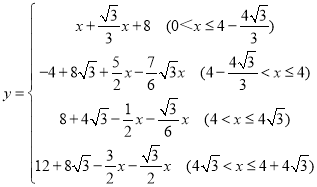 ;
;

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案