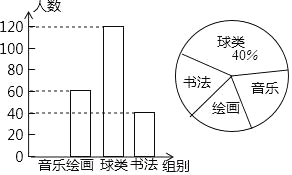
题目内容
【题目】如图，直线L1：y=bx+c与抛物线L2：y=ax2的两个交点坐标分别为A（m，4），B（1，1）．
（1）求m的值；
（2）过动点P（n，0）且垂直于x轴的直线与L1，L2的交点分别为C，D，当点C位于点D上方时，请直接写出n的取值范围．
【答案】（1）-2；（2）﹣2＜n＜1．
【解析】试题分析：（1）将点B坐标代入抛物线解析式求出a，再将点A坐标代入即可求出m的值；（2）当点C位于点D上方时，即直线在抛物线的上方便可，根据图象判断此时n的取值范围.
解：（1）把B（1，1）代入y=ax2，得a=1，
∴抛物线解析式为y=x2．
把A（m，4）代入y=x2，得4=m2，
∴m=±2．
∵点A在第二象限，
∴m=﹣2；
（2）观察函数图象可知：当﹣2＜x＜1时，直线在抛物线的上方，
∴n的取值范围为﹣2＜n＜1．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
【题目】某商场计划购进A，B两种新型节能台灯共120盏，这两种台灯的进价、售价如表所示：
类型 价格 | 进价（元/盏） | 售价（元/盏） |
A型 | 30 | 45 |
B型 | 50 | 70 |
（1）若商场预计进货款为5200元，则这两种台灯各购进多少盏？
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
