题目内容
【题目】如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
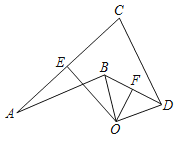
【答案】∠OBD=41°.
【解析】
连接OA,OC,根据线段垂直平分线的性质得到OA=OC,OB=OD,证明△ABO≌△COD,根据全等三角形的性质得到∠ABO=∠CDO,设∠OBD=∠ODB=α,∠ABO=∠CDO=β,解方程组即可求出∠OBD.
解:连接OA,OC,
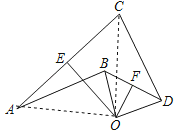
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD,
∵AB=CD,
∴△ABO≌△COD(SSS),
∴∠ABO=∠CDO,
设∠OBD=∠ODB=α,∠ABO=∠CDO=β,
∴α+β=120°,β﹣α=38°,
∴α=41°,
∴∠OBD=41°.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目