Question

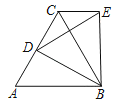
【题目】如图，点D是等边△ABC的边AC上一点，以BD为边作等边△BDE，点C，E在BD同侧，下列结论：①∠ABD＝30°；②CE∥AB；③CB平分∠ACE；④CE＝AD，其中错误的有（　　）

A.0个B.1个C.2个D.3个

Answer 1

【答案】B

【解析】

结合等边三角形的性质和全等三角形的判定与性质，分别对各个结论进行推理判断即可．

解：∵△ABC和△BDE是等边三角形，

∴∠A＝∠ACB＝∠ABC＝∠DBE＝60°，AB＝BC，BD＝BE，

∴∠ABD＝∠CBE，①不正确；

在△ABD和△CBE中，

，

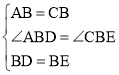∴△ABD≌△CBE（SAS），

∴∠A＝∠BCE＝60°，AD＝CE，④正确；

∴∠BCE＝∠ABC，

∴CE∥AB，②正确；

∵∠CBE＝∠ACB＝60°，

∴CB平分∠ACE，③正确；

∴错误的有1个，

故选：B．