题目内容
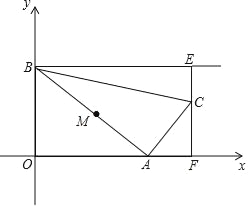
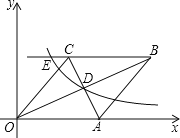
【题目】已知如图,四边形OABC为菱形,A点的坐标为![]() ,对角线OB、AC相交于D点,双曲线
,对角线OB、AC相交于D点,双曲线![]() 经过D点,交BC的延长线于E点,且
经过D点,交BC的延长线于E点,且![]() ,则E点的坐标是
,则E点的坐标是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:作DH⊥x轴于H,BG⊥x轴于G,根据菱形的面积等于对角线乘积的一半得到菱形OABC的面积=![]() OBAC=
OBAC=![]() ×160=80;则△ODA的面积为20,根据三角形面积公式可计算出DA=4,再根据菱形的性质易得DH为△OBG的中位线,则BG=8,所以E点的纵坐标为8;接着证明Rt△DOH∽Rt△ADH,得到DH2=OHAH,由于DH=4,AH=10-OH,则OH(10-OH)=16,解得OH=8或OH=2(舍去),可确定D点坐标为(8,4),利用待定系数法得到反比例函数解析式为,同时可确定E点坐标.
×160=80;则△ODA的面积为20,根据三角形面积公式可计算出DA=4,再根据菱形的性质易得DH为△OBG的中位线,则BG=8,所以E点的纵坐标为8;接着证明Rt△DOH∽Rt△ADH,得到DH2=OHAH,由于DH=4,AH=10-OH,则OH(10-OH)=16,解得OH=8或OH=2(舍去),可确定D点坐标为(8,4),利用待定系数法得到反比例函数解析式为,同时可确定E点坐标.
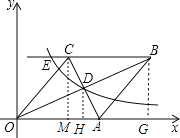
详解:作DH⊥x轴于H,BG⊥x轴于G,如图,
∵四边形OABC为菱形, ∴菱形OABC的面积=![]() OBAC=
OBAC=![]() ×160=80,
×160=80,
∴![]() DHOA=菱形OABC的面积的
DHOA=菱形OABC的面积的![]() =
=![]() ×80, 而A点的坐标为(10,0),
×80, 而A点的坐标为(10,0),
∴![]() DH×10=
DH×10=![]() ×80, ∴DH=4, ∵OB与AC互相垂直平分,
×80, ∴DH=4, ∵OB与AC互相垂直平分,
∴∠ADO=90°,DH为△OBG的中位线, ∴BG=2DH=8, ∴E点的纵坐标为8,
∵∠DOH+∠ODH=∠ODH+∠ADH=90°,∴∠DOH=∠ADH,
∴Rt△DOH∽Rt△ADH, ∴DH:AH=OH:DH,即DH2=OHAH,
∵DH=4,AH=OA-OH=10-OH, ∴OH(10-OH)=16,解得OH=8或OH=2(舍去),
∴D点坐标为(8,4), 把D(8,4)代入y=![]() 得k=4×8=32,
得k=4×8=32,
∴反比例函数解析式为y=![]() , 把y=8代入得
, 把y=8代入得![]() =8,解得x=4, ∴E点坐标为(4,8).
=8,解得x=4, ∴E点坐标为(4,8).

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】为了加强公民的节水意识,合理利用水资源,我市采用价格调控的手段达到节水的目的,我市自来水收费的价目表如下表:
价目表 | |
每月用水量 | 单价 |
不超出6m3的部分 | 3元/m3 |
超出6m3不超出10m3的部分 | 5元/m3 |
超出10m3的部分 | 9元/m3 |
注:水费按月结算 | |
请根据如表的内容解答下列问题:
(1)填空:若该户居民2月份用水4m3,则应收水费_______元;
(2)若该户居民3月份用水am3(其中6m3<a<10m3),则应收水费多少元?(用含a的代数式表示,并化简)
(3)若该户居民4、5两个月共用水15m3(5月份用水量超过了4月份),设4月份用水xm3,求该户居民4、5两个月共交水费多少元?(用含x的代数式表示,并化简)