题目内容
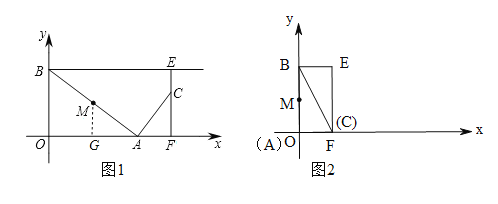
【题目】如图,点A是x轴非负半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.
(Ⅰ)当t=2时,求点M的坐标;
(Ⅱ)设ABCE的面积为S,当点C在线段EF上时,求S与t之间的函数关系式,并写出自变量t的取值范围;
(Ⅲ)当t为何值时,BC+CA取得最小值.
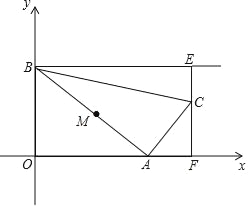
【答案】(1)(1,2);(2)S=![]() t+8(0≤t≤8);(3)当t=0时,BC+AC有最小值
t+8(0≤t≤8);(3)当t=0时,BC+AC有最小值
【解析】试题分析:(I)过M作MG⊥OF于G,分别求OG和MG的长即可;
(II)如图1,同理可求得AG和OG的长,证明△AMG≌△CAF,得:AG=CF=![]() t,AF=MG=2,分别表示EC和BE的长,代入面积公式可求得S与t的关系式;并求其t的取值范围;
t,AF=MG=2,分别表示EC和BE的长,代入面积公式可求得S与t的关系式;并求其t的取值范围;
(III)证明△ABO∽△CAF,根据勾股定理表示AC和BC的长,计算其和,根据二次根式的意义得出当t=0时,值最小.
试题解析:解:(I)如图1,过M作MG⊥OF于G,∴MG∥OB,当t=2时,OA=2.∵M是AB的中点,∴G是AO的中点,∴OG=![]() OA=1,MG是△AOB的中位线,∴MG=
OA=1,MG是△AOB的中位线,∴MG=![]() OB=
OB=![]() ×4=2,∴M(1,2);
×4=2,∴M(1,2);
(II)如图1,同理得:OG=AG=![]() t.∵∠BAC=90°,∴∠BAO+∠CAF=90°.∵∠CAF+∠ACF=90°,∴∠BAO=∠ACF.∵∠MGA=∠AFC=90°,MA=AC,∴△AMG≌△CAF,∴AG=CF=
t.∵∠BAC=90°,∴∠BAO+∠CAF=90°.∵∠CAF+∠ACF=90°,∴∠BAO=∠ACF.∵∠MGA=∠AFC=90°,MA=AC,∴△AMG≌△CAF,∴AG=CF=![]() t,AF=MG=2,∴EC=4﹣
t,AF=MG=2,∴EC=4﹣![]() t,BE=OF=t+2,∴S△BCE=
t,BE=OF=t+2,∴S△BCE=![]() ECBE=
ECBE=![]() (4﹣
(4﹣![]() t)(t+2)=﹣
t)(t+2)=﹣![]() t2+
t2+![]() t+4;
t+4;
S△ABC=![]() ABAC=
ABAC=![]()
![]()
![]() =
=![]() t2+4,∴S=S△BEC+S△ABC=
t2+4,∴S=S△BEC+S△ABC=![]() t+8.
t+8.
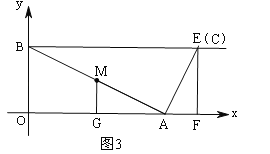
当A与O重合,C与F重合,如图2,此时t=0,当C与E重合时,如图3,AG=EF,即 ![]() t=4,t=8,∴S与t之间的函数关系式为:S=
t=4,t=8,∴S与t之间的函数关系式为:S=![]() t+8(0≤t≤8);
t+8(0≤t≤8);
(III)如图1,易得△ABO∽△CAF,∴![]() =
=![]() =
=![]() =2,∴AF=2,CF=
=2,∴AF=2,CF=![]() t,由勾股定理得:AC=
t,由勾股定理得:AC=![]() =
=![]() =
=![]() ,BC=
,BC=![]() =
=![]() =
=![]() ,∴BC+AC=(
,∴BC+AC=( ![]() +1)
+1)![]() ,∴当t=0时,BC+AC有最小值.
,∴当t=0时,BC+AC有最小值.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】地球运动是同学们非常喜欢的日常体育运动,为了更合理地配置体育运动器材和场地,某校针对“你最喜欢的球类运动”进行了一次随机抽样调查(每名被调查者分别选一项球类运动),并把调查结果绘制成如图的两个统计图表(不完整).
某校学生最喜爱的球类运动统计表
最喜爱的球类运动 | 人数 |
足球 | 27 |
篮球 |
|
乒乓球 | 24 |
羽毛球 | 24 |
排球 |
|
某校学生最喜爱的球类运动统计图

请根据所给信息,解答下列问题:
(1)本次被抽样调查的学生共有多少人?
(2)求扇形统计图中最喜爱篮球部分的圆心角度数;
(3)若该校共有学生960人,请根据抽样结果估计学生中最喜爱乒乓球的人数.