题目内容
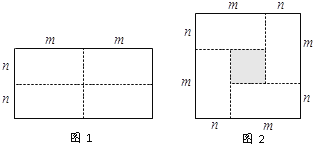
【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的方法拼成一个边长为(m+n)的正方形.
⑴ 请用两种不同的方法求图2中阴影部分的面积.
方法1: ;方法2: ;
⑵ 观察图2写出![]() ,
,![]() ,
,![]() 三个代数式之间的等量关系: ;
三个代数式之间的等量关系: ;
⑶ 根据⑵中你发现的等量关系,解决如下问题:若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() -4
-4![]() ;
; ![]() ;(2)
;(2)![]() =
=![]() -4
-4![]() ;(3)61
;(3)61
【解析】
(1)直接计算小正方形的边长可得面积,或者用大正方形面积减去四个小长方形面积来表示;
(2)它们都表示阴影部分小正方形的面积,故相等;
(3)由(2)得出的关系式变形即可得结果.
⑴ 方法1:由图形可知,大正方形面积减去四个小长方形面积来表示即为阴影部分面积,大正方形边长为![]() ,则大正方形面积为
,则大正方形面积为![]() ,所以阴影部分面积为
,所以阴影部分面积为![]() ;
;
方法2:阴影部分为正方形,边长为![]() ,故面积可表示为
,故面积可表示为![]() ;
;
⑵ ![]() 与
与![]() 都表示同一个图形面积,
都表示同一个图形面积,
所以![]() =
=![]() -4
-4![]() ;
;
⑶ 由(2)可得![]() =
=![]() -4
-4![]() =
=![]() =61
=61

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目